Objectively comparing pro audio signal processing products is often impossible. Missing on too many data sheets are the conditions used to obtain the published data. Audio specifications come with conditions. Tests are not performed in a vacuum with random parameters. They are conducted using rigorous procedures and the conditions must be stated along with the test results.
To understand the conditions, you must first understand the tests. This note introduces the classic audio tests used to characterize audio performance. It describes each test and the conditions necessary to conduct the test.
Apologies are made for the many abbreviations, terms and jargon necessary to tell the story. Please make liberal use of Rane's Pro Audio Reference to help decipher things. Also, note that when the term impedance is used, it is assumed a constant pure resistance, unless otherwise stated.
The accompanying table (back page) summarizes common audio specifications and their required conditions. Each test is described next in the order of appearance in the table.
By its name you know it is a measure of unwanted signals. Distortion is the name given to anything that alters a pure input signal in any way other than changing its magnitude. The most common forms of distortion are unwanted components or artifacts added to the original signal, including random and hum-related noise. A spectral analysis of the output shows these unwanted components. If a piece of gear is perfect the spectrum of the output shows only the original signal -- nothing else -- no added components, no added noise -- nothing but the original signal. The following tests are designed to measure different forms of audio distortion.
What is tested? A form of nonlinearity that causes unwanted signals to be added to the input signal that are harmonically related to it. The spectrum of the output shows added frequency components at 2x the original signal, 3x, 4x, 5x, and so on, but no components at, say, 2.6x the original, or any fractional multiplier, only whole number multipliers.
How is it measured? This technique excites the unit with a single high purity sine wave and then examines the output for evidence of any frequencies other than the one applied. Performing a spectral analysis on this signal (using a spectrum, or FFT analyzer) shows that in addition to the original input sine wave, there are components at harmonic intervals of the input frequency. Total harmonic distortion (THD) is then defined as the ratio of the rms voltage of the harmonics to that of the fundamental component. This is accomplished by using a spectrum analyzer to obtain the level of each harmonic and performing an rms summation. The level is then divided by the fundamental level, and cited as the total harmonic distortion (expressed in percent). Measuring individual harmonics with precision is difficult, tedious, and not commonly done; consequently, THD+N (see below) is the more common test. Caveat Emptor: THD+N is always going to be a larger number than just plain THD. For this reason, unscrupulous (or clever, depending on your viewpoint) manufacturers choose to spec just THD, instead of the more meaningful and easily compared THD+N.
Required Conditions. Since individual harmonic amplitudes are measured, the manufacturer must state the test signal frequency, its level, and the gain conditions set on the tested unit, as well as the number of harmonics measured. Hopefully, it's obvious to the reader that the THD of a 10 kHz signal at a +20 dBu level using maximum gain, is apt to differ from the THD of a 1 kHz signal at a -10 dBV level and unity gain. And more different yet, if one manufacturer measures two harmonics while another measures five.
Full disclosure specs will test harmonic distortion over the entire 20 Hz to 20 kHz audio range (this is done easily by sweeping and plotting the results), at the pro audio level of +4 dBu. For all signal processing equipment, except mic preamps, the preferred gain setting is unity. For mic pre amps, the standard practice is to use maximum gain. Too often THD is spec'd only at 1 kHz, or worst, with no mention of frequency at all, and nothing about level or gain settings, let alone harmonic count.
Correct: THD (5th-order) less than 0.01%, +4 dBu, 20-20 kHz, unity gain
Wrong: THD less than 0.01%
What is tested? Similar to the THD test above, except instead of measuring individual harmonics this tests measures everything added to the input signal. This is a wonderful test since everything that comes out of the unit that isn't the pure test signal is measured and included -- harmonics, hum, noise, RFI, buzz ... everything.
How is it measured? THD+N is the rms summation of all signal components (excluding the fundamental) over some prescribed bandwidth. Distortion analyzers make this measurement by removing the fundamental (using a deep and narrow notch filter) and measuring what's left using a bandwidth filter (typically 22 kHz, 30 kHz or 80 kHz). The remainder contains harmonics as well as random noise and other artifacts.
Weighting filters are rarely used. When they are used, too often it is to hide pronounced AC mains hum artifacts. An exception is the strong argument to use the ITU-R (CCIR) 468 curve because of its proven correlation to what is heard. However, since it adds 12 dB of gain in the critical midband (the whole point) it makes THD+N measurements bigger, so marketeers prevent its widespread use.
[Historical Note: Many old distortion analyzers labeled "THD" actually measured THD+N.]
Required Conditions. Same as THD (frequency, level & gain settings), except instead of stating the number of harmonics measured, the residual noise bandwidth is spec'd, along with whatever weighting filter was used. The preferred value is a 20 kHz (or 22 kHz) measurement bandwidth, and "flat," i.e., no weighting filter.
Conflicting views exist regarding THD+N bandwidth measurements. One argument goes: it makes no sense to measure THD at 20 kHz if your measurement bandwidth doesn't include the harmonics. Valid point, and one supported by the IEC, which says that THD should not be tested any higher than 6 kHz, if measuring five harmonics using a 30 kHz bandwidth, or 10 kHz, if only measuring the first three harmonics. Another argument states that since most people can't even hear the fundamental at 20 kHz, let alone the second harmonic, there is no need to measure anything beyond 20 kHz. Fair enough. However, the case is made that using an 80 kHz bandwidth is crucial, not because of 20 kHz harmonics, but because it reveals other artifacts that can indicate high frequency problems. All true points, but competition being what it is, standardizing on publishing THD+N figures measured flat over 22 kHz seems justified, while still using an 80 kHz bandwidth during the design, development and manufacturing stages.
Correct: THD+N less than 0.01%, +4 dBu, 20-20 kHz, unity gain, 20 kHz BW
Wrong: THD less than 0.01%
What is tested? A more meaningful test than THD, intermodulation distortion gives a measure of distortion products not harmonically related to the pure signal. This is important since these artifacts make music sound harsh and unpleasant.
Intermodulation distortion testing was first adopted in the U.S. as a practical procedure in the motion picture industry in 1939 by the Society of Motion Picture Engineers (SMPE -- no "T" [television] yet) and made into a standard in 1941.
How is it measured? The test signal is a low frequency (60 Hz) and a non-harmonically related high frequency (7 kHz) tone, summed together in a 4:1 amplitude ratio. (Other frequencies and amplitude ratios are used; for example, DIN favors 250 Hz & 8 kHz.) This signal is applied to the unit, and the output signal is examined for modulation of the upper frequency by the low frequency tone. As with harmonic distortion measurement, this is done with a spectrum analyzer or a dedicated intermodulation distortion analyzer. The modulation components of the upper signal appear as sidebands spaced at multiples of the lower frequency tone. The amplitudes of the sidebands are rms summed and expressed as a percentage of the upper frequency level.
[Noise has little effect on SMPTE measurements because the test uses a low pass filter that sets the measurement bandwidth, thus restricting noise components; therefore there is no need for an "IM+N" test.]
Required Conditions. SMPTE specifies this test use 60 Hz and 7 kHz combined in a 12 dB ratio (4:1) and that the peak value of the signal be stated along with the results. Strictly speaking, all that needs stating is "SMPTE IM" and the peak value used. However, measuring the peak value is difficult. Alternatively, a common method is to set the low frequency tone (60 Hz) for +4 dBu and then mixing the 7 kHz tone at a value of -8 dBu (12 dB less).
Correct: IMD (SMPTE) less than 0.01%, 60Hz/7kHz, 4:1, +4 dBu
Wrong: IMD less than 0.01%
What is tested? This tests for non-harmonic nonlinearities, using two equal amplitude, closely spaced, high frequency tones, and looking for beat frequencies between them. Use of beat frequencies for distortion detection dates back to work first documented in Germany in 1929, but was not considered a standard until 1937, when the CCIF (International Telephonic Consultative Committee) recommend the test. [This test is often mistakenly referred to as the CCIR method (as opposed to the CCIF method). A mistake compounded by the many correct audio references to the CCIR 468 weighting filter.] Ultimately, the CCIF became the radiocommunications sector (ITU-R) of the ITU (International Telecommunications Union), therefore the test is now known as the IMD (ITU-R).
How is it measured? The common test signal is a pair of equal amplitude tones spaced 1 kHz apart. Nonlinearity in the unit causes intermodulation products between the two signals. These are found by subtracting the two tones to find the first location at 1 kHz, then subtracting the second tone from twice the first tone, and then turning around and subtracting the first tone from twice the second, and so on. Usually only the first two or three components are measured, but for the oft-seen case of 19 kHz and 20 kHz, only the 1 kHz component is measured.
Required Conditions. Many variations exist for this test. Therefore, the manufacturer needs to clearly spell out the two frequencies used, and their level. The ratio is understood to be 1:1.
Correct: IMD (ITU-R) less than 0.01%, 19 kHz/20 kHz, 1:1, +4 dBu
Wrong: IMD less than 0.01%
What is tested? This specification indirectly tells you how noisy a unit is. S/N is calculated by measuring a unit's output noise, with no signal present, and all controls set to a prescribed manner. This figure is used to calculate a ratio between it and a fixed output reference signal, with the result expressed in dB.
How is it measured? No input signal is used, however the input is not left open, or unterminated. The usual practice is to leave the unit connected to the signal generator (with its low output impedance) set for zero volts. Alternatively, a resistor equal to the expected driving impedance is connected between the inputs. The magnitude of the output noise is measured using an rms-detecting voltmeter. Noise voltage is a function of bandwidth -- wider the bandwidth, the greater the noise. This is an inescapable physical fact. Thus, a bandwidth is selected for the measuring voltmeter. If this is not done, the noise voltage measures extremely high, but does not correlate well with what is heard. The most common bandwidth seen is 22 kHz (the extra 2 kHz allows the bandwidth-limiting filter to take affect without reducing the response at 20 kHz). This is called a "flat" measurement, since all frequencies are measured equally.
Alternatively, noise filters, or weighting filters, are used when measuring noise. Most often seen is A-weighting, but a more accurate one is called the ITU-R (old CCIR) 468 filter. This filter is preferred because it shapes the measured noise in a way that relates well with what's heard.
Pro audio equipment often lists an A-weighted noise spec -- not because it correlates well with our hearing -- but because it can "hide" nasty hum components that make for bad noise specs. Always wonder if a manufacturer is hiding something when you see A-weighting specs. While noise filters are entirely appropriate and even desired when measuring other types of noise, it is an abuse to use them to disguise equipment hum problems. A-weighting rolls off the low-end, thus reducing the most annoying 2nd and 3rd line harmonics by about 20 dB and 12 dB respectively. Sometimes A-weighting can "improve" a noise spec by 10 dB.
The argument used to justify this is that the ear is not sensitive to low frequencies at low levels (à la Fletcher-Munson equal loudness curves), but that argument is false. Fletcher-Munson curves document equal loudness of single tones. Their curve tells us nothing of the ear's astonishing ability to sync in and lock onto repetitive tones -- like hum components -- even when these tones lie beneath the noise floor. This is what A-weighting can hide. For this reason most manufacturers shy from using it; instead they spec S/N figures "flat" or use the ITU-R 468 curve (which actually makes their numbers look worse, but correlate better with the real world).
However, an exception has arisen: Digital products using A/D and D/A converters regularly spec S/N and dynamic range using A-weighting. This follows the semiconductor industry's practice of spec'ing delta-sigma data converters A-weighted. They do this because they use clever noise shaping tricks to create 24-bit converters with acceptable noise behavior. All these tricks squeeze the noise out of the audio bandwidth and push it up into the higher inaudible frequencies. The noise may be inaudible, but it is still measurable and can give misleading results unless limited. When used this way, the A-weighting filter rolls off the high frequency noise better than the flat 22 kHz filter and compares better with the listening experience. The fact that the low-end also rolls off is irrelevant in this application. (See Digital Dharma of Audio A/D Converters)
Required Conditions. In order for the published figure to have any meaning, it must include the measurement bandwidth, including any weighting filters and the reference signal level. Stating that a unit has a "S/N = 90 dB" is meaningless without knowing what the signal level is, and over what bandwidth the noise was measured. For example if one product references S/N to their maximum output level of, say, +20 dBu, and another product has the same stated 90 dB S/N, but their reference level is + 4 dBu, then the second product is, in fact, 16 dB quieter. Likewise, you cannot accurately compare numbers if one unit is measured over a BW of 80 kHz and another uses 20 kHz, or if one is measured flat and the other uses A-weighting. By far however, the most common problem is not stating any conditions.
Correct: S/N = 90 dB re +4 dBu, 22 kHz BW, unity gain
Wrong: S/N = 90 dB
What is tested? Equivalent input noise, or input referred noise, is how noise is spec'd on mixing consoles, standalone mic preamps and other signal processing units with mic inputs. The problem in measuring mixing consoles (and all mic preamps) is knowing ahead of time how much gain is going to be used. The mic stage itself is the dominant noise generator; therefore, the output noise is almost totally determined by the amount of gain: turn the gain up, and the output noise goes up accordingly. Thus, the EIN is the amount of noise added to the input signal. Both are then amplified to obtain the final output signal.
For example, say your mixer has an EIN of -130 dBu. This means the noise is 130 dB below a reference point of 0.775 volts (0 dBu). If your microphone puts out, say, -50 dBu under normal conditions, then the S/N at the input to the mic preamp is 80 dB (i.e., the added noise is 80 dB below the input signal). This is uniquely determined by the magnitude of the input signal and the EIN. From here on out, turning up the gain increases both the signal and the noise by the same amount.
How is it measured? With the gain set for maximum and the input terminated with the expected source impedance, the output noise is measured with an rms voltmeter fitted with a bandwidth or weighting filter.
Required Conditions. This is a spec where test conditions are critical. It is very easy to deceive without them. Since high-gain mic stages greatly amplify source noise, the terminating input resistance must be stated. Two equally quiet inputs will measure vastly different if not using the identical input impedance. The standard source impedance is 150 ohms. As unintuitive as it may be, a plain resistor, hooked up to nothing, generates noise, and the larger the resistor value the greater the noise. It is called thermal noise or Johnson noise (after its discoverer J. B. Johnson, in 1928) and results from the motion of electron charge of the atoms making up the resistor. All that moving about is called thermal agitation (caused by heat -- the hotter the resistor, the noisier).
The input terminating resistor defines the lower limit of noise performance. In use, a mic stage cannot be quieter than the source. A trick which unscrupulous manufacturers may use is to spec their mic stage with the input shorted -- a big no-no, since it does not represent the real performance of the preamp.
The next biggie in spec'ing the EIN of mic stages is bandwidth. This same thermal noise limit of the input terminating resistance is a strong function of measurement bandwidth. For example, the noise voltage generated by the standard 150 ohm input resistor, measured over a bandwidth of 20 kHz (and room temperature) is -131 dBu, i.e., you cannot have an operating mic stage, with a 150 ohm source, quieter than -131 dBu. However, if you use only a 10 kHz bandwidth, then the noise drops to -134 dBu, a big 3 dB improvement. (For those paying close attention: it is not 6 dB like you might expect since the bandwidth is half. It is a square root function, so it is reduced by the square root of one-half, or 0.707, which is 3 dB less).
Since the measured output noise is such a strong function of bandwidth and gain, it is recommended to use no weighting filters. They only complicate comparison among manufacturers. Remember: if a manufacturer's reported EIN seems too good to be true, look for the details. They may not be lying, only using favorable conditions to deceive.
Correct: EIN = -130 dBu, 22 kHz BW, max gain, Rs = 150 ohms
Wrong: EIN = -130 dBu
What is tested? The unit's bandwidth or the range of frequencies it passes. All frequencies above and below a unit's Frequency Response are attenuated -- sometimes severely.
How is it measured? A 1 kHz tone of high purity and precise amplitude is applied to the unit and the output measured using a dB-calibrated rms voltmeter. This value is set as the 0 dB reference point. Next, the generator is swept upward in frequency (from the 1 kHz reference point) keeping the source amplitude precisely constant, until it is reduced in level by the amount specified. This point becomes the upper frequency limit. The test generator is then swept down in frequency from 1 kHz until the lower frequency limit is found by the same means.
Required Conditions. The reduction in output level is relative to 1 kHz; therefore, the 1 kHz level establishes the 0 dB point. What you need to know is how far down is the response where the manufacturer measured it. Is it 0.5 dB, 3 dB, or (among loudspeaker manufacturers) 10 dB?
Note that there is no discussion of an increase, that is, no mention of the amplitude rising. If a unit's frequency response rises at any point, especially the endpoints, it indicates a fundamental instability problem and you should run from the store. Properly designed solid-state audio equipment does not ever gain in amplitude when set for flat response (tubes or valve designs using output transformers are a different story and are not dealt with here). If you have ever wondered why manufacturers state a limit of "+0 dB", that is why. The preferred condition here is at least 20 Hz to 20 kHz measured +0/-0.5 dB.
Correct: Frequency Response = 20-20 kHz, +0/-0.5 dB
Wrong: Frequency Response = 20-20 kHz
What is tested? This gives a measure of a balanced input stage's ability to reject common-mode signals. Common-mode is the name given to signals applied simultaneously to both inputs. Normal differential signals arrive as a pair of equal voltages that are opposite in polarity: one applied to the positive input and the other to the negative input. A common-mode signal drives both inputs with the same polarity. It is the job of a well designed balanced input stage to amplify differential signals, while simultaneously rejecting common-mode signals. Most common-mode signals result from RFI (radio frequency interference) and EMI (electromagnetic interference, e.g., hum and buzz) signals inducing themselves into the connecting cable. Since most cables consist of a tightly twisted pair, the interfering signals are induced equally into each wire. The other big contributors to common-mode signals are power supply and ground related problems between the source and the balanced input stage.
How is it measured? Either the unit is adjusted for unity gain, or its gain is first determined and noted. Next, a generator is hooked up to drive both inputs simultaneously through two equal and carefully matched source resistors valued at one-half the expected source resistance, i.e., each input is driven from one-half the normal source impedance. The output of the balanced stage is measured using an rms voltmeter and noted. A ratio is calculated by dividing the generator input voltage by the measured output voltage. This ratio is then multiplied by the gain of the unit, and the answer expressed in dB.
Required Conditions. The results may be frequency-dependent, therefore, the manufacturer must state the frequency tested along with the CMR figure. Most manufacturers spec this at 1 kHz for comparison reasons. The results are assumed constant for all input levels, unless stated otherwise.
Correct: CMRR = 40 dB @ 1 kHz
Wrong: CMRR = 40 dB
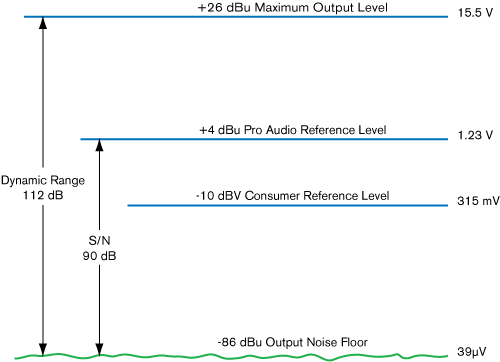
What is tested? First, the maximum output voltage and then the output noise floor are measured and their ratio expressed in dB. Sounds simple and it is simple, but you still have to be careful when comparing units.
How is it measured? The maximum output voltage is measured as described below, and the output noise floor is measured using an rms voltmeter fitted with a bandwidth filter (with the input generator set for zero volts). A ratio is formed and the result expressed in dB.
Required Conditions. Since this is the ratio of the maximum output signal to the noise floor, then the manufacturer must state what the maximum level is, otherwise, you have no way to evaluate the significance of the number. If one company says their product has a dynamic range of 120 dB and another says theirs is 126 dB, before you jump to buy the bigger number, first ask, "Relative to what?" Second, ask, "Measured over what bandwidth, and were any weighting filters used?" You cannot know which is better without knowing the required conditions.
Again, beware of A-weighted specs. Use of A-weighting should only appear in dynamic range specs for digital products with data converters (see discussion under S/N). For instance, using it to spec dynamic range in an analog product may indicate the unit has hum components that might otherwise restrict the dynamic range.
Correct: Dynamic Range = 120 dB re +26 dBu, 22 kHz BW
Wrong: Dynamic Range = 120 dB
What is tested? Signals from one channel leaking into another channel. This happens between independent channels as well as between left and right stereo channels, or between all six channels of a 5.1 surround processor, for instance.
How is it measured? A generator drives one channel and this channel's output value is noted; meanwhile the other channel is set for zero volts (its generator is left hooked up, but turned to zero, or alternatively the input is terminated with the expect source impedance). Under no circumstances is the measured channel left open. Whatever signal is induced into the tested channel is measured at its output with an rms voltmeter and noted. A ratio is formed by dividing the unwanted signal by the above-noted output test value, and the answer expressed in dB. Since the ratio is always less than one (crosstalk is always less than the original signal) the expression results in negative dB ratings. For example, a crosstalk spec of -60 dB is interpreted to mean the unwanted signal is 60 dB below the test signal.
Required Conditions. Most crosstalk results from printed circuit board traces "talking" to each other. The mechanism is capacitive coupling between the closely spaced traces and layers. This makes it strongly frequency dependent, with a characteristic rise of 6 dB/octave, i.e., the crosstalk gets worst at a 6 dB/octave rate with increasing frequency. Therefore knowing the frequency used for testing is essential. And if it is only spec'd at 1 kHz (very common) then you can predict what it may be for higher frequencies. For instance, using the example from above of a -60 dB rating, say, at 1 kHz, then the crosstalk at 16 kHz probably degrades to -36 dB. But don't panic, the reason this usually isn't a problem is that the signal level at high frequencies is also reduced by about the same 6 dB/octave rate, so the overall S/N ratio isn't affected much.
Another important point is that crosstalk is assumed level independent unless otherwise noted. This is because the parasitic capacitors formed by the traces are uniquely determined by the layout geometry, not the strength of the signal.
Correct: Crosstalk = -60 dB, 20-20kHz, +4 dBu, channel-to-channel
Wrong: Crosstalk = -60 dB
What is tested? Input impedance measures the load that the unit represents to the driving source, while output impedance measures the source impedance that drives the next unit.
How is it measured? Rarely are these values actually measured. Usually they are determined by inspection and analysis of the final schematic and stated as a pure resistance in ohms. Input and output reactive elements are usually small enough to be ignored. (Phono input stages and other inputs designed for specific load reactance are exceptions.)
Required Conditions. The only required information is whether the stated impedance is balanced or unbalanced (balanced impedances usually are exactly twice unbalanced ones). For clarity when spec'ing balanced circuits, it is preferred to state whether the resistance is "floating" (exists between the two lines) or is ground referenced (exists from each line to ground).
The impedances are assumed constant for all frequencies within the unit's bandwidth and for all signal levels, unless stated otherwise. (Note that while this is true for input impedances, most output impedances are, in fact, frequency-dependent -- some heavily.)
Correct: Input Impedance = 20k ohms, balanced line-to-line
Wrong: Input Impedance = 20k ohms
What is tested? The input stage is measured to establish the maximum signal level in dBu that causes clipping or specified level of distortion.
How is it measured? During the final product process, the design engineer uses an adjustable 1 kHz input signal, an oscilloscope and a distortion analyzer. In the field, apply a 1 kHz source, and while viewing the output, increase the input signal until visible clipping is observed. It is essential that all downstream gain and level controls be set low enough that you are assured the applied signal is clipping just the first stage. Check this by turning each level control and verifying that the clipped waveform just gets bigger or smaller and does not ever reduce the clipping.
Required Conditions. Whether the applied signal is balanced or unbalanced and the amount of distortion or clipping used to establish the maximum must be stated. The preferred value is balanced and 1% distortion, but often manufacturers use "visible clipping," which is as much as 10% distortion, and creates a false impression that the input stage can handle signals a few dB hotter than it really can. No one would accept 10% distortion at the measurement point, so to hide it, it is not stated at all -- only the max value given without conditions. Buyer beware.
The results are assumed constant for all frequencies within the unit's bandwidth and for all levels of input, unless stated otherwise.
Correct: Maximum Input Level = +20 dBu, balanced, <1% THD
Wrong: Maximum Input Level = +20 dBu
What is tested? The unit's output is measured to establish the maximum signal possible before visible clipping or a specified level of distortion.
How is it measured? The output is fixed with a standard load resistor and measured either balanced or unbalanced, using an oscilloscope and a distortion analyzer. A 1 kHz input signal is increased in amplitude until the output measures the specified amount of distortion, and that value is expressed in dBu. Next, the signal is swept through the entire audio range to check that this level does not change with frequency.
Required Conditions. Two important issues are present here: The first is the need to know whether a unit can swing enough unclipped volts for your application. The second is more difficult and potentially more serious, and that is the unit's ability to drive long lines without stability problems, or frequency loss.
The manufacturer must state whether the spec is for balanced or unbalanced use (usually balanced operation results in 6 dB more swing); what distortion was used for determination (with the preferred value being 1% THD); over what frequency range is this spec valid (prefer 20 Hz -- 20 kHz; watch out for just 1 kHz specs); and what load impedance is guaranteed (2k ohms or greater is preferred; 600 ohm operation is obsolete and no longer required except for specialized applications, with broadcast and telecommunications noted as two of them).
This last item applies only to signal processing units designed as line drivers: These should specify a max cable length and the specs of the cable -- by either specific brand & type, or give the max cable capacitance in pF/meter.
Correct: Max Output Level = +26 dBu balanced, 20-20 kHz, >2k ohms, <1% THD
Wrong: Max Output Level = +26 dBu
What is tested? The ratio of the largest possible output signal as compared to a fixed input signal, expressed in dB, is called the Maximum Gain of a unit.
How is it measured? With all level & gain controls set maximum, and for an input of 1 kHz at an average level that does not clip the output, the output of the unit is measured using an rms voltmeter. The output level is divided by the input level and the result expressed in dB.
Required Conditions. There is nothing controversial here, but confusion results if the test results do not clearly state whether the test was done using balanced or unbalanced outputs. Often a unit's gain differs 6 dB between balanced and unbalanced hook-up. Note that it usually does not change the gain if the input is driven balanced or unbalanced, only the output connection is significant.
The results are assumed constant for all frequencies within the unit's bandwidth and for all levels of input, unless stated otherwise.
Correct: Maximum Gain = +6 dB, balanced-in to balanced-out
Wrong: Maximum Gain = +6 dB
Specifications Require Conditions Accurate audio measurements are difficult and expensive. To purchase the test equipment necessary to perform all the tests described here would cost you a minimum of $10,000. And that price is for computer-controlled analog test equipment, if you want the cool digital-based, dual domain stuff -- double it. This is why virtually all purchasers of pro audio equipment must rely on the honesty and integrity of the manufacturers involved, and the accuracy and completeness of their data sheets and sales materials.
Tolerances or Limits Another caveat for the informed buyer is to always look for tolerances or worst-case limits associated with the specs. Limits are rare, but they are the gristle that gives specifications truth. When you see specs without limits, ask yourself, is this manufacturer NOT going to ship the product if it does not exactly meet the printed spec? Of course not. The product will ship, and probably by the hundreds. So what is the real limit? At what point will the product not ship? If it's off by 3 dB, or 5%, or 100 Hz ... what? When does the manufacturer say no? The only way you can know is if they publish specification tolerances and limits.
Correct: S/N = 90 dB (± 2 dB), re +4 dBu, 22 kHz BW, unity gain
Wrong: S/N = 90 dB
Common Signal Processing Specs With Required Conditions |
||||
Abbr |
Name |
|
Required Conditions |
Preferred Values* |
THD |
Total Harmonic Distortion |
|
Frequency |
20 Hz - 20 kHz |
THD+N |
Total Harmonic Distortion plus Noise |
|
Frequency |
20 Hz - 20 kHz |
IM or IMD |
Intermodulation Distortion (SMPTE method) |
|
Type |
SMPTE |
IM or IMD |
Intermodulation Distortion (ITU-R method) |
|
Type |
ITU-R (or Difference-Tone) |
S/N or SNR |
Signal-to-Noise Ratio |
|
Reference Level |
re +4 dBu |
EIN |
Equivalent Input Noise or Input Referred Noise |
|
Input Terminating Impedance |
150 ohms |
BW |
Frequency Response |
|
Level Change re 1 kHz |
+0/-0.5 dB (or +0/-3 dB) |
CMR or CMRR |
Common Mode Rejection or Common Mode Rejection Ratio |
|
Frequency (Assumed independent of level, unless noted otherwise.) |
1 kHz |
-- |
Dynamic Range |
|
Maximum Output Level |
+26 dBu |
-- |
Crosstalk (as –dB) |
|
Frequency |
20 Hz - 20 kHz |
-- |
Input & Output Impedance |
|
Balanced or Unbalanced |
Balanced |
-- |
Maximum Input Level |
|
Balanced or Unbalanced |
Balanced 1% |
-- |
Maximum Output Level |
|
Balanced or Unbalanced |
Balanced |
-- |
Maximum Gain |
|
Balanced or Unbalanced Output (Assumed constant over full BW & at all levels, unless otherwise noted.) |
Balanced |
|
||||
Portions of this note appeared previously in the May/June & Sep/Oct 2000 issues of LIVESOUND! International magazine reproduced here with permission.