Why DSP Boxes Set the Same Way Differ

Why DSP Boxes Set the Same Way Differ

Ray Miller, DSP Consultant

RaneNote 167, ©2007 Rane Corporation

• Different Bandwidth Definitions
• Comparison Between Manufacturers
• Testing Tips
• The Mathematics Behind DSP Differences

Introduction

A common pro audio problem is that if you input the same settings into different manufacturer’s programmable parametric equalizer sections on processor boxes or control programs, they produce different results; some more so than others. This makes comparing DSP platforms difficult.

The explanation is simple: manufacturers use different definitions of filter bandwidth.

Understanding this is not as simple, as explained here.

The proliferation of loudspeaker processing units demonstrates that the differing definitions of bandwidth gets thorny when one manufacturer develops filters for use in a DSP box made by another manufacturer, and the end user is attempting to implement them in a DSP unit made by a third manufacturer. Frustration ensues.

It is important to note this isn’t a digital problem or a DSP problem. It is a definition problem. Indeed, analog parametric equalizers are just as prone to head-to-head comparisons as DSP units, and for the same reasons. For an experiment, make matching settings on different analog parametric EQs and run a response curve for each. Comparing them may surprise you.

The same is true for digital processors. Corresponding amplitude and frequency settings will track closely; it is the bandwidth settings where things get sticky.

Bell Filter (“Bandwidth”) Definitions

A significant inconvenience in the audio industry today is that filter bandwidth is defined in several different ways. You cannot expect two pieces of equipment set the same way to have the same frequency response.

Filter bandwidth is not even set the same way: it may be set in octaves or Q.

It is not even widely known what to expect in a particular case. There is an incentive to become familiar with one device or manufacturer and avoid change, even when it would be good for other reasons. It’s not always even possible to get two equalizers to have the same frequency response, but you can usually get close.

Many parametric equalizers use cascaded second-order bandpass filters, which makes their responses add in dB -- then each band can be treated independently. Given a way to convert one type of bandwidth to another, different equalizers of this general type can be set so that the responses match, limited only by the resolution of the bandwidth control.

The pro audio industry needs to promote understanding of the issues and to determine what each manufacturer is doing. Also, it is reasonably easy to test equalizers to determine what the bandwidth definition is, and that will be covered here.

Only a handful of definitions are in use and once these are well known, it becomes possible to use equipment with differing definitions, and ultimately the matching process could be automated.

Isn’t There One Definition of Bandwidth?

As long as bandwidth refers to just a frequency range, there is essentially one definition, although it has several forms. The standard ones are hertz, Q, and octaves, and well-known formulas exist to convert one to another. Octaves and Q have the advantage of being independent of the filter center frequency. Here are some definitions:

(Frequency Span in Hz) = (High Frequency) – (Low Frequency)

Q = (Center Frequency) / (Frequency Span in Hz)

2octaves = (High Frequency) / (Low Frequency)

Multiple definitions come into play when the endpoints of the frequency range refer to a particular level on a filter magnitude response curve, such as "3 dB down," and result largely from the possible choices for this level.

Historically, bandwidth was defined for a bandpass filter, and referred to the difference between the frequencies where the passband dropped to –3 dB (see Figure 1).

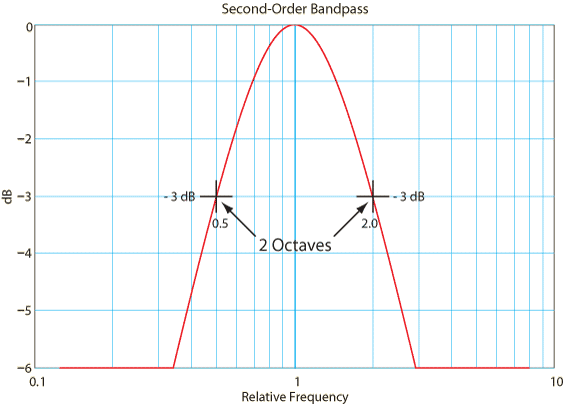
Figure 1. Most common bandwidth definition.

As shown in Figure 1, the bandpass has a 2 octave bandwidth, and the Q is 1/ (2-0.5) = 2/3. If the center frequency were 1000 Hz, the bandwidth would be 2000 Hz – 500 Hz = 1500 Hz.

Choosing a level other than –3 dB changes the definition of bandwidth for a given filter response, and therefore changes the filter response for a given bandwidth setting. The Linkwitz-Riley crossover is one example of a filter where the –3 dB point is not used; the –6 dB point is used instead.

Overview of the Bell Filter Situation

What we see and refer to as "bandwidth" in parametric equalizers is called a "Bell filter" due to its shape. Strictly speaking, it is not a true bandpass filter in an engineering sense, although it is made from one.

A second-order Bell filter, which is one of a cascaded set of filters, is equivalent to a second-order bandpass filter (with a given Q) summed back with the original signal as shown in Figure 2.

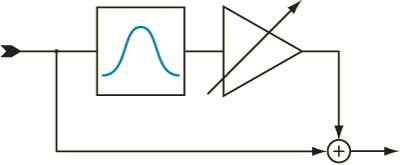
Figure 2. Creating a Bell curve from a bandpass filter.

However, the Bell curve always has a larger bandwidth than its corresponding bandpass filter, taken at any appropriate reference gain, such as –3 dB from peak. Figure 3 shows a Bell filter response superimposed on the bandpass from which it can be constructed. Notice the widening of the Bell response. Technically, the bandpass in this construction has been shifted up 6 dB for the purpose of comparison.

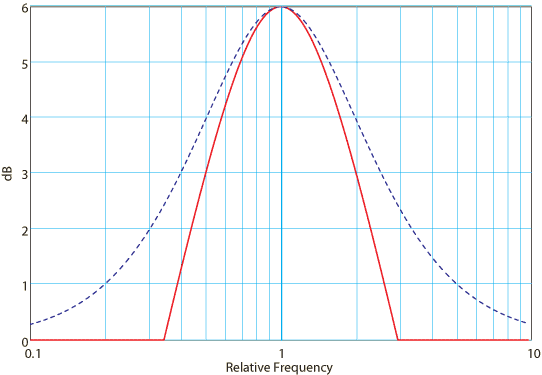
Figure 3. Comparison between Bell and bandpass curves.

One definition currently in use simply sets the bandpass from the filter bandwidth setting (referred to here as Bandpass Q). Or you can compensate by using a smaller (fixed) bandwidth, which narrows the Bell so the bandwidth is correct for one setting. This effective technique has been used historically in analog constant-Q equalizers, and the result is very nearly constant compared to proportional-Q equalizers.

The use of microprocessors and DSP have made other approaches more practical, where filter bandwidth is automatically adjusted in various ways to achieve particular filter gains at the frequencies corresponding to the bandwidth.

What are the Other Definitions?

The other definitions will be described here using the term Filter Gain, to mean the gain for the Bell filter at either frequency at the endpoints of the bandwidth. Instead of considering the bandpass response, a reasonable definition is to make the (Bell) Filter Gain –3 dB from the peak. But if, for example, a filter response only ranges from 0 dB to +2 dB, it’s impossible to use a –3 dB response point. The Bell filter has this dilemma for small settings. This is remedied by choosing the filter gain to be one-half of the peak (setting) dB for settings under 6 dB. At 6 dB, these two definitions agree, and this will be referred to as the 3 dB Hybrid method here. Figure 4 is a graph of the Bell filter curves. Note that the 3 dB Hybrid method (dotted) is 3 dB down at the bandwidth (solid horizontal lines), for settings 6 dB or higher.

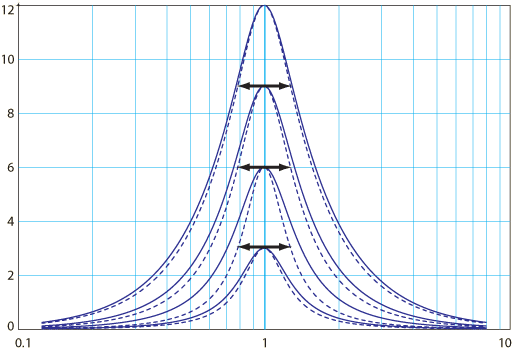
Figure 4. Bandpass Q definition vs. hybrid (3 dB and dB/2).

Another definition sets the bandwidth such that filter gain is one-half of the peak always, which is a consistent definition that results in a comparatively narrower response curve for large settings. It will be called the dB/2 method.

The particular definition is sometimes chosen to be different when the Bell filter is attenuating (cutting) rather than providing gain (boosting). Many manufacturers treat the two the same way, yielding a symmetrical response between boost and cut, but others set the bandwidth smaller for cutting filters, such as by forcing the Filter Gain to be –3 dB from unity gain. For low bandwidth settings, this results in a notch filter.

What are Particular Manufacturers Doing?

The author knows Rane uses Bandpass-Q (so far), has information from EAW, and has tested products from QSC, dbx, Biamp, and Shure. There is also some information about XTA, Ashley, Symetrix and BSS, but not verified at this time. It is quite possible that a given manufacturer has not always applied the same definition. Figures 5 and 6 compare some definitions, the first showing the filter gain (in absolute dB, at the bandwidth edge frequencies) versus setting (mentally turn it over and it looks more familiar). The second shows the Q of a bandpass that could construct the filter (set to a Q of one, or equivalent setting of 1.3885 octaves), versus filter gain setting.

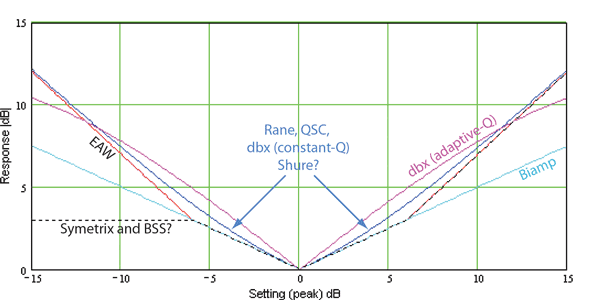
Figure 5. Filter gain versus setting for various manufacturers.

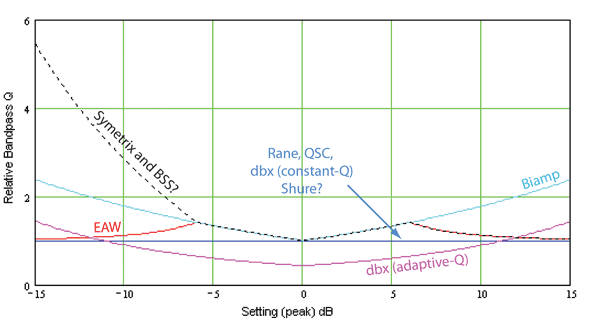
Figure 6. Q versus gain setting for results shown in Figure 5.

The dB response graph reveals definitions based on dB response versus setting: Biamp, with dB/2, and the 3 dB Hybrid: EAW and others, including possibly Symetrix and BSS. Although it’s not obvious, the unusual dBx adaptive-Q seems to be based on dB response, and may be characterized by the following equation for response dB at bandwidth endpoints versus setting dB:

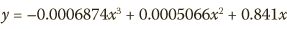
At a setting of 12 dB, this is approximately 3 dB down. dbx refers to this response as emulating mixing console EQ.

The bandpass Q graph reveals the constant bandpass Q definition of Rane, QSC, Shure, and dbx (constant-Q).

Other Aspects

Individual filters can be combined in different ways, such as cascaded or parallel, and while this has little or no impact on the response of a single filter, two or more filters are a different story. Only cascaded filters are considered here, and this characteristic can easily be tested.

So far, the issues apply both to analog and digital filters, but digital filter response becomes more asymmetrical as frequencies affected by the filter approach the Nyquist limit (24 kHz for 48 k sample rate), complicating the bandwidth issue. This effect can be tolerated (ignored), or it can be countered in different ways. Usually the gain drops to unity at the Nyquist, but there is a difficult method for designing digital bell filters that are much more symmetrical, and they don’t drop to unity gain at the Nyquist. Even so, all DSP products must apply a filter below the Nyquist, and so typically there is a sharp cutoff with linear (or near-linear) phase at 23 kHz, "chopping off" the filter response abruptly.

A related issue is how the frequency response is shown in software. The author has found that the digital effects just mentioned are not shown by all manufacturers, so might either be corrected or ignored. The Biamp Audia appears to be correcting the actual response.

Equipment Testing

Testing is quite simple but involves a bit of mathematics to understand the results.

Connect the equipment to a signal generator and detector (e.g., Audio Precision or equivalent), and be sure that the only processing is from the parametric filter(s) being adjusted (no crossover, compressor, etc). Check for interaction between filters, by setting two filters (call them A and B) so that they both affect a frequency, and measure with just A, just B, and both. The result for both should be the sum of the readings for A and for B. In that case, testing one filter is sufficient, and otherwise the situation becomes more complicated, and is not covered here.

To test a single filter, set it at a frequency well below the Nyquist, such as 1 kHz, measure at one frequency chosen as one that will vary significantly, and record the level for a collection of settings. A good choice is a generator frequency of 707 Hz with the filter set to 1.0 octave, as that will immediately reveal a dB response filter type, such as dB/2. Be careful that readings aren’t affected by clipping or noise. A collection of -12, -11 … -1, 0, 1… 11, 12 should be more than sufficient. You can use intervals of two or three dB, but it can help in some cases to have extra data. One bandwidth setting should also be sufficient. Additional measurements can be taken, such as for several bandwidth settings. Measurement at the 0 dB setting is included only as a check of equipment gain.

From these numbers, you can tell if the definitions agree for boost and cut, and if they don’t, consider boost and cut as separate cases. If the numbers are nearly equal, the difference can be due to measurement error.

Using the octaves or Q setting, you can determine either bandwidth end frequency. The generator/measurement frequency should be chosen to be close to one of these in order to minimize the effect of measurement error. Below are formulas for the finding the lower frequency and for converting between octaves and Q.

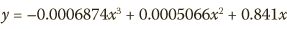
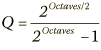
If the measurement frequency is chosen to be either endpoint of the bandwidth (such as 707 Hz for a 1 kHz, 1.0 octave filter), it may immediately reveal a pattern such as 3 dB from setting, or (dB/2). If so, you are done. If no such pattern is revealed, the next step is to determine the bandpass Q at each setting from the following formula. Use the readings ‘M’ from each setting ‘g’. If a reading M is larger than the setting ‘g’ because of a measurement error, it must not be used in this equation. Also, settings and readings in dB need to be converted by g, M = 10^0.05dB

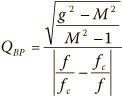, where g is the setting, f is the generator frequency, fc is the center frequency, and M is the measurement. This works for any frequency, f, different than fc, and its derivation is given later, where:

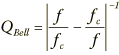
If the bandpass Q is found to be nearly constant, the equipment is using the bandpass Q definition. The Q error needs to be attributable to measurement error. The author has investigated the error sensitivity. Assume that the measurement error is 0.01 dB. If a bandwidth end frequency is used, the Q is 1.4, and the absolute value of the setting is at least 4 dB, the Q error will be below 0.01. Settings from 1 dB to 3 dB can result in errors up to 0.03. Error increases with increasing Q. Choosing other reasonable measurement frequencies increases the error slightly.

Whether the bandpass Q is constant or not, the entire filter response can be calculated from the bandpass Q. No matter what your measurement frequency, you can now calculate the response at either bandwidth end frequency using the following formula:

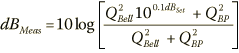
Where Q_Bell is defined above. This can immediately reveal a pattern mentioned earlier, such as -3 dB.

Some definitions won’t be clear from testing, but can be characterized anyway using a table or curve fit for dB or bandpass Q as a function of setting, as was done above for dbx (adaptive-Q).

Mathematical Analysis

Here lies the complete mathematical analysis of the above results and becomes quite involved. It is provided for DSP designers and the mathematically curious.

When the filter has a peak greater than unity gain (boost), it is equivalent to a scaled bandpass plus one (see Figure 1). The case where the peak is less than unity gain (cut) has a transfer function that is the reciprocal of the first case. This is equivalent to both the filter’s dB setting and magnitude response in dB having a sign reversal. Therefore, results for the boost case apply to the cut case.

All filters are assumed to be designed for an angular (or radian) frequency, ω, of one; other design frequencies require a substitution into these equations of:

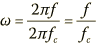
The (analog) Bell filter has the following transfer function, constructed from a bandpass:

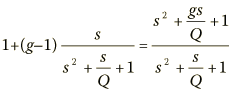
Notice that Q here is that of a bandpass filter. Evaluating at s = jω and taking the squared-magnitude yields:

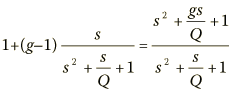
Bandpass Q is a measure of frequency span where at either frequency at the ends of the span, the bandpass magnitude response is down 3 dB, easily shown to be given by this function of the end frequencies (if the angular design frequency is one):

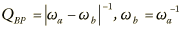
We can define another type of Q; call it Q_Bell, which is a function of a frequency where we consider the magnitude response of the Bell filter curve (possibly a bandwidth end frequency):

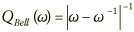
Then substituting into the squared-magnitude response results in:

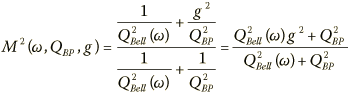
Given a setting g and a desired or measured magnitude M which may be for instance 0.7071*g for 3 dB down from the peak, we can solve for the bandpass Q needed to achieve a desired Bell Q:

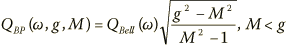
Q_Bell may be defined to be a specific bandwidth where the Bell magnitude is controlled, or can be a function of an arbitrary measurement frequency. It is important to remember the value of M depends on the particular meaning of Q_Bell.

We can of course solve for Q_Bell, given a Bandpass Q, which may be a function of g:

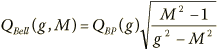
Given a definition where M is some complicated function of g, M = M(g), the general formulas can be applied. Here are some simplifications:

dB/2
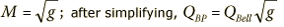3 dB Down
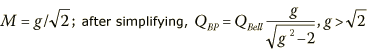3 dB (up)

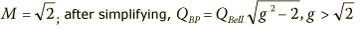Given the bandpass Q, the response at any frequency is found using the equation for M² converting from/to dB.

Summary

Bandwidth definitions can be determined for many parametric equalizers, making it practical to transfer settings between devices with different definitions. This is limited only by control resolution. There are only a handful of definitions, so sometimes conversion won’t be required. Testing to determine the definition is not difficult, and can support claims by manufacturers.

Conversion Calculator

Rane has created an Excel conversion calculator for use in inputting EAW Q values into Rane DSP parametrics. Other manufacturers may be included in the future.

EAW to Rane Parametric Q Converter (zipped) for Microsoft Excel.

Second-order bandpass filters are those described by a transfer function having quadratic equations in the numerator and denominator. A quadratic equation is one in which the first term is squared, having the general form ax²+ bx + c = 0, where a, b, and c are constants.

"Why DSP Boxes Set the Same Way Differ" Download this note in PDF.