Knowledge Base
Linkwitz-Riley Crossovers: A Primer
Linkwitz-Riley Crossovers: A Primer
Dennis Bohn, Rane Corporation
RaneNote 160, written October 2005
- Linkwitz-Riley Background
- 1st-Order Crossover Networks
- Butterworth Crossovers 2nd to 4th-Order
- Linkwitz-Riley Crossovers 2nd to 8th-Order
- Phase, Transient & Power Responses
Introduction
In 1976, Siegfried Linkwitz published his famous paper [1] on active crossovers for non-coincident drivers. In it, he credited Russ Riley (a co-worker and friend) with contributing the idea that cascaded Butterworth filters met all Linkwitz's crossover requirements. Their efforts became known as the Linkwitz-Riley (LR) crossover alignment. In 1983, the first commercially available Linkwitz-Riley active crossovers appeared from Sundholm and Rane.
Today, the de facto standard for professional audio active crossovers is the 4th-order Linkwitz-Riley (LR-4) design. Offering in-phase outputs and steep 24 dB/octave slopes, the LR-4 alignment gives users the necessary tool to scale the next step toward the elusive goal of perfect sound. And many DSP crossovers offer an 8th-order Linkwitz-Riley (LR-8) option.
Before exploring the math and electronics of LR designs, it is instructional to review just what Linkwitz-Riley alignments are, and how they differ from traditional Butterworth designs.
Linkwitz-Riley Crossovers: Background
Siegfried Linkwitz and Russ Riley, then two Hewlett-Packard R&D engineers, wrote the aforementioned paper describing a better mousetrap in crossover design. Largely ignored (or unread) for several years, it eventually received the attention it deserved. Typical of truly useful technical papers, it is very straightforward and unassuming: a product of careful analytical attention to details, with a wonderfully simple solution.
It is seldom whether to cross over, but rather, how to cross over. Over the years active crossovers proliferated at a rate equal to the proverbial lucky charm.
In 1983, a 4th-order state variable active filter [2] was developed by Rane Corporation to implement the Linkwitz-Riley alignment for crossover coefficients and now forms the heart of many analog active crossover designs.
A Perfect Crossover
Mother Nature gets the blame. Another universe, another system of physics, and the quest for a perfect crossover might not be so difficult. But we exist here and must make the best of what we have. And what we have is the physics of sound, and of electromagnetic transformation systems that obey these physics.
A perfect crossover, in essence, is no crossover at all. It would be one driver that could reproduce all frequencies equally well. Since we cannot have that, second best would be multiple speakers, along the same axis, with sound being emitted from the same point, i.e., a coaxial speaker that has no time shift between drivers. This gets closer to being possible, but still is elusive. Third best, and this is where we really begin, are multiple drivers mounted one above the other with no time shift, i.e., non-coincident drivers adjusted front-to-rear to compensate for their different points of sound propagation. Each driver would be fed only the frequencies it is capable of reproducing. The frequency dividing network would be, in reality, a frequency gate. It would have no phase shift or time delay. Its amplitude response would be absolutely flat and its roll-off characteristics would be the proverbial brick wall. (Brings a tear to your eye, doesn't it?)
DSP digital technology makes such a crossover possible, but not at analog prices demanded by most working musicians.
Linkwitz-Riley Crossover
What distinguishes the Linkwitz-Riley crossover design from others is its perfect combined radiation pattern of the two drivers at the crossover point. Stanley P. Lipshitz [3] coined the term "lobing error" to describe this crossover characteristic. It derives from the examination of the acoustic output plots (at crossover) of the combined radiation pattern of the two drivers (see Figures 1 & 2). If it is not perfect the pattern forms a lobe that exhibits an off-axis frequency dependent tilt with amplitude peaking.
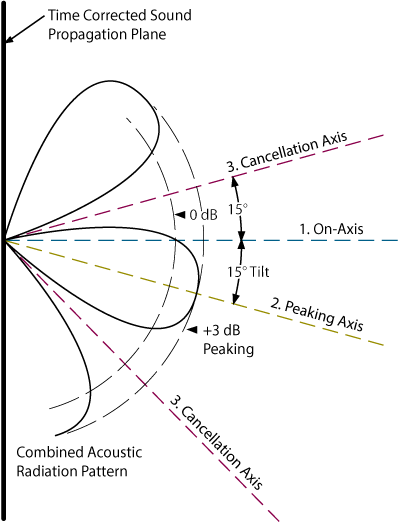
Figure 1a
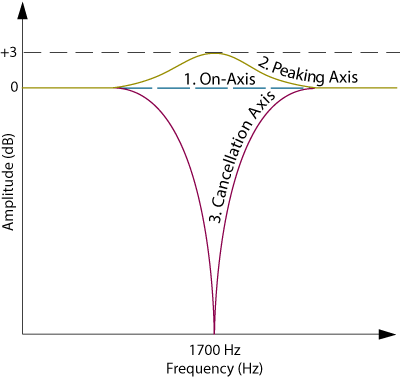
Figure 1b
Figure 1. Butterworth all-pass design radiation pattern at crossover.
Interpretation of Figure 1 is not particularly obvious. Let's back up a minute and add some more details. For simplicity, only a two way system is being modeled. The two drivers are mounted along the vertical center of the enclosure (there is no side-to-side displacement, i.e., one driver is mounted on top of the other.) All front-to-back time delay between drivers is corrected. The figure shown is a polar plot of the sideview, i.e., the angles are vertical angles.
It is only the vertical displacement sound field that is at issue here. All of the popular crossover types (constant voltage [4], Butterworth all-pass [5], etc.) are well behaved along the horizontal on-axis plane. To illustrate the geometry involved here, imagine attaching a string to the speaker at the mid-point between the drivers. Position the speaker such that the mid-point is exactly at ear level. Now pull the string taut and hold it up to your nose (go on, no one's looking). The string should be parallel to the floor. Holding the string tight, move to the left and right: this is the horizontal on-axis plane. Along this listening plane, all of the classic crossover designs exhibit no problems. It is when you lower or raise your head below or above this plane that the problems arise. This is the crux of Siegfried Linkwitz's contribution to crossover design. After all these years and as hard as it is to believe, he was the first person to publish an analysis of what happens off-axis with non-coincident drivers (not-coaxial). (Others may have done it before, but it was never made public record.)
Figure 1a represents a side view of the combined acoustic radiation pattern of the two drivers emitting the same single frequency. That is, a plot of what is going on at the single crossover frequency all along the vertical plane. The pattern shown is for the popular 18 dB/octave Butterworth all-pass design with a crossover frequency of 1700 Hz and drivers mounted 7 inches apart1.
What is seen is a series of peaking and cancellation nodes. Back to the string: holding it taut again and parallel to the floor puts you on-axis. Figure 1a tells us that the magnitude of the emitted 1700 Hz tone will be 0 dB (a nominal reference point). As you lower your head, the tone increases in loudness until a 3 dB peak is reached at 15 degrees below parallel. Raising your head above the on-axis line causes a reduction in magnitude until 15 degrees is reached where there is a complete cancellation of the tone. There is another cancellation axis located 49 degrees below the on-axis. Figure 1b depicts the frequency response of the three axes for reference.
For a constant voltage design, the response looks worse, having a 6 dB peaking axis located at -20 degrees and the cancellation axes at +10 and -56 degrees, respectively. The peaking axis tilts toward the lagging driver in both cases, due to phase shift between the two crossover outputs.
The cancellation nodes are not due to the crossover design, they are due to the vertically displaced drivers. (The crossover design controls where cancellation nodes occur, not that they occur.) The fact that the drivers are not coaxial means that any vertical deviation from the on-axis line results in a slight, but very significant difference in path lengths to the listener. This difference in distance traveled is effectively a phase shift between the drivers. And this causes cancellation nodes -- the greater the distance between drivers, the more nodes.
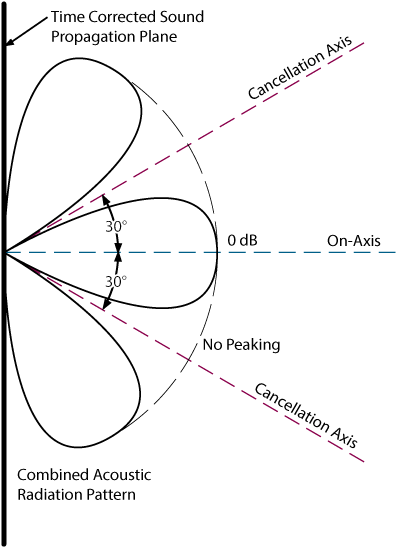
Figure 2. Linkwitz-Riley radiation response at crossover.
In distinct contrast to these examples is Figure 2, where the combined response of a Linkwitz-Riley crossover design is shown. There is no tilt and no peaking -- just a perfect response whose only limitation is the dispersion characteristics of the drivers. The main contributor to this ideal response is the in-phase relationship between the crossover outputs.
Two of the cancellation nodes are still present, but are well defined and always symmetrical about the on-axis plane. Their location changes with crossover frequency and driver mounting geometry (distance between drivers). With the other designs, the peaking and cancellation axes change with frequency and driver spacing.
Let's drop the string and move out into the audience to see how these cancellation and peaking nodes affect things. Figure 3 shows a terribly simplified, but not too inaccurate stage-audience relationship with the characteristics of Figure 1 added.
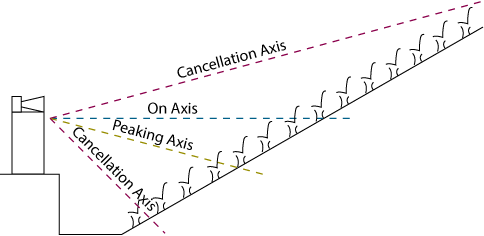
Figure 3. Butterworth all-pass crossover stage-audience relationship.
The band is cooking and then comes to a musical break. All eyes are on the flautist, who immediately goes into her world-famous 1700 Hz solo. So what happens? The people in the middle hear it sweet, while those up front are blown out of their seats, and those in the back are wondering what the hell all the fuss is!
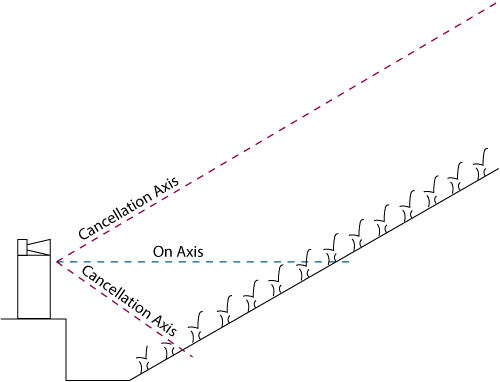
Figure 4. Linkwitz-Riley crossover stage-audience relationship.
Figure 4 shows the identical situation but with the Linkwitz-Riley characteristics of Figure 2 added. Now the people in the middle still hear everything sweet, but those up front are not blown away, and those in the back understand the fuss!
I think you get the point.
Now let's get real. I mean really real. The system isn't two way, it is four way. There isn't one enclosure, there are sixteen. No way are the drivers 7 inches apart -- try 27 inches. And time corrected? Fuhgeddaboudit.
Can you even begin to imagine what the vertical off-axis response will look like with classic crossover designs? The further apart the drivers are, the greater the number of peaks and cancellations, resulting in a multi-lobe radiation pattern. Each crossover frequency has its own set of patterns, complicated by each enclosure contributing even more patterns. And so on.
(For large driver spacing the Linkwitz-Riley design has as many lobes as other designs, except that the peaks are always 0 dB, and the main lobe is always on-axis.)
Note that all this is dealing with the direct sound field, no multiple secondary arrivals or room interference or reverberation times are being considered. Is it any wonder that when you move your real-time analyzer microphone three feet you get a totally different response?
Now let me state clearly that using a Linkwitz-Riley crossover will not solve all these problems. But it will go a long way toward that goal.
The other outstanding characteristic of the Linkwitz-Riley alignment is the rolloff rate of 24 dB/octave (Figure 5). With such a sharp drop-off, drivers can operate closer to their theoretical crossover points without the induced distortion normally caused by frequencies lying outside their capabilities. Frequencies just one octave away from the crossover point are already attenuated by 24 dB (a factor or about 1/16). The importance of sharp cutoff rate and in-phase frequency response of the crossover circuitry cannot be over-stressed in contributing to smooth overall system response.
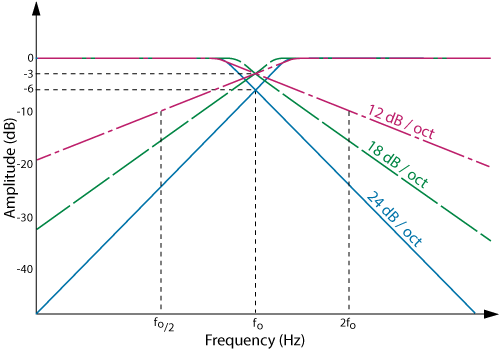
Figure 5. Frequency response of 4th-order Linkwitz-Riley crossover.
A summary of the characteristics of a Linkwitz-Riley crossover:
1. Absolutely flat amplitude response throughout the passband with a steep 24 dB/octave rolloff rate after the crossover point.
2. The acoustic sum of the two driver responses is unity at crossover. (Amplitude response of each is -6 dB at crossover, i.e., there is no peaking in the summed acoustic output.)
3. Zero phase difference between drivers at crossover. (Lobing error equals zero, i.e., no tilt to the polar radiation pattern.) In addition, the phase difference of zero degrees through crossover places the lobe of the summed acoustic output on axis at all frequencies.
4. The low pass and high pass outputs are everywhere in phase. (This guarantees symmetry of the polar response about the crossover point.)
5. All drivers are always wired the same (in phase).
A casual reading of the above list may suggest that this is, indeed, the perfect crossover. But such is not so. The wrinkle involves what is known as "linear phase." A Linkwitz-Riley crossover alignment is not linear phase: meaning that the amount of phase shift is a function of frequency. Or, put into time domain terms, the amount of time delay through the filter is not constant for all frequencies, which means that some frequencies are delayed more than others. (In technical terms, the network has a frequency-dependent group delay, but with a gradually changing characteristic.)
Is this a problem? Specifically, is this an audible "problem?" In a word, no.
Much research has been done on this question [6-9] with approximately the same conclusions: given a slowly changing non-linear phase system, the audible results are so minimal as to be nonexistent; especially in the face of all of the other system nonlinearities. And with real-world music sources (remember music?), it is not audible at all.
State-Variable Solution
One of the many attractions of the Linkwitz-Riley design is its utter simplicity, requiring only two standard 2nd-order Butterworth filters in series. The complexities occur when adjustable crossover frequencies are required.
After examining and rejecting all of the standard approaches to accomplish this task, Rane developed a 4th-order state-variable filter specifically for implementing the Linkwitz-Riley crossover. The state-variable topology was chosen over other designs for the following reasons:
1. It provides simultaneous high-pass and low-pass outputs that are always at exactly the same frequency.
2. Changing frequencies can be done simultaneously on the high-pass and low-pass outputs without any changes in amplitude or Q (quality factor).
3. The sensitivities of the filter are very low. (Sensitivity is a measure of the effects of non-ideal components on an otherwise, ideal response.)
4. It offers the most cost-effective way to implement two 4th-order responses with continuously variable crossover frequencies.
Time or Phase Correction
Implicit in the development of the theory of a Linkwitz-Riley crossover design is the key assumption that the sound from each driver radiates from the some exact vertical plane, i.e., that the drivers have no time delay with respect to each other. The crossover then prohibits any lobing errors as the sound advances forward simultaneously from the two drivers. Figure 6 illustrates such a front-to-back displacement, which causes the lobing error shown in Figure 7a.
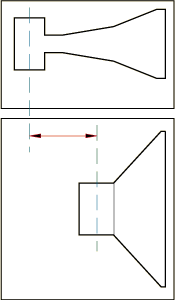
Figure 6. Driver Displacement
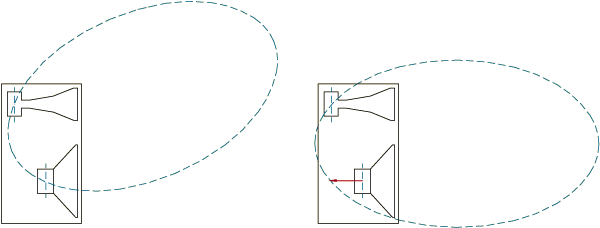
Figure 7a. Without time alignment - - - - - - Figure 7b. With time alignment
Figure 7. Adding delay to the forward driver time-aligns the phase of both drivers, reducing lobing error.
A Linkwitz-Riley crossover applied to drivers that are not time-corrected loses most of its magic. The lobing error is no longer zero; it exhibits a frequency dependent tilt with magnitude errors as shown in Figure 7a.
Crossover Primer
1st-Order Network
Analog crossovers begin with a resistor and a capacitor. It never gets more complicated than that -- just resistors and capacitors: lots and lots of resistors and capacitors. Resistors are the great emancipators of electronics; they are free of frequency dependence. They dissipate energy without frequency prejudice. All frequencies treated equally. Capacitors, on the other hand, selectively absorb energy; they store it, to be released at a later time. While resistors react instantly to any voltage changes within a circuit, capacitors take time to charge and discharge.
Capacitors are so frequency dependent they only pass signals with frequency associated with them. Direct-current (think of it as zero frequency) will not pass at all, while at the other end of the spectrum very high frequencies will not absorb. Capacitors act like a piece of wire to high frequencies; hardly there at all.
We use these facts to create a crossover network. Figure 8 shows such a circuit. By interchanging the positions of the resistor and capacitor, low-pass (low frequencies = LF) and high-pass (high frequencies = HF) filters result. For the low-pass case (LF), the capacitor ignores low frequencies and shunts all high frequencies to ground. For the high-pass case (HF), the opposite occurs. All low frequencies are blocked and only high frequencies are passed.
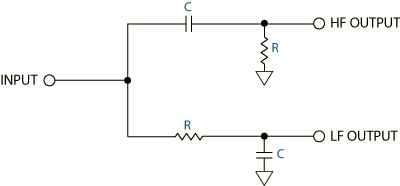
Figure 8. 1st-order crossover network
1st-Order Amplitude Response
Using 1 kHz as an example and plotting the amplitude versus frequency response (Figure 9) reveals the expected low-pass and high-pass shapes. Figure 9 shows that the 1st-order circuit exhibits 6 dB/octave slopes. Also, that 6 dB/octave equals 20 dB/decade. Both ways of expressing steepness are useful and should be memorized. The rule is: each order, or degree, of a filter increases the slopes by 6 dB/octave or 20 dB/decade. So, for example, a 4th-order (or 4th-degree -- interchangeable terms) circuit has 24 dB/octave (4 x 6 dB/octave) or 80 dB/decade (4 x 20 dB/decade) slopes.
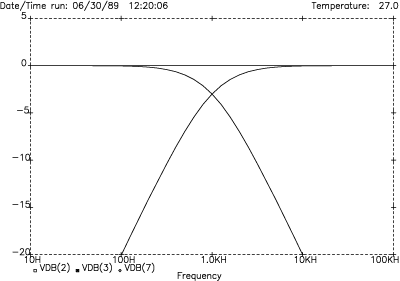
Figure 9. 1st-order amplitude response
Using equal valued resistors and capacitors in each of the circuits causes the amplitude responses to "cross over" at one particular frequency where their respective -3 dB points intersect. This point represents the attenuation effect resulting when the impedance of the capacitor equals the resistance of the resistor.
The equivalent multiplying factor for -3 dB is .707, i.e., a signal attenuated by 3 dB will be .707 times the original in level. Ohms law tells us that if the voltage is multiplied by .707, then the current will also be multiplied by .707. Power is calculated by multiplying voltage times current. Therefore, a voltage multiplied by .707, and a current multiplied by .707, equals 0.5 power. So the -3 dB points represent the half-power point -- a useful reference.
Lastly, Figure 9 shows the flat amplitude response resulting from summing the LF and HF outputs together. This is called constant voltage, since the result of adding the two output voltages together equals a constant. The 1st-order case is ideal in that constant power also results. Constant-power refers to the summed power response for each loudspeaker driver operating at the crossover frequency. This, too, results in a constant. Since each driver operates at half-power at the crossover frequency, their sum equals one--or unity, a constant.
1st-Order Phase Response
Much is learned by examining the phase shift behavior (Figure 10) of the 1st-order circuit. The upper curve is the HF output and the lower curve is the LF output. The HF curve starts at +90° phase shift at DC, reduces to +45° at the crossover frequency and then levels out at 0o for high frequencies. The LF curve starts with 0° phase shift at DC, has -45° at the crossover frequency and levels out at -90° for high frequencies.
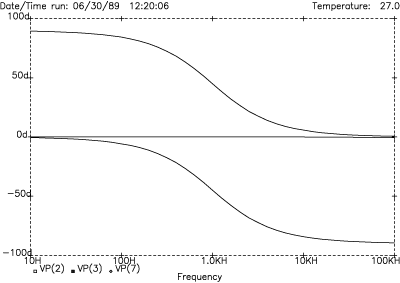
Figure 10. 1st-order phase response
Because of its reactive (energy storing) nature each capacitor in a circuit contributes 90° of phase shift, either positive or negative depending upon its application. Since the HF section places the capacitor directly in the signal path, this circuit starts out with +90° phase shift. This is called phase lead. The LF section, which starts out with 0° and eventually becomes -90° is called phase lag.
Examination of Figure 10 allows us to formulate a new rule: each order, or degree, of a crossover network contributes ±45° of phase shift at the crossover frequency (positive for the HF output and negative for the LF output).
Once again, Figure 10 shows the idealized nature of the 1st-order case. Here the result of summing the outputs together produces 0° phase shift, which is to say that the summed amplitude and phase shift of a 1st-order crossover is equivalent to a piece of wire.
1st-Order Group Delay Response
We shall return to our rules shortly, but first the concept of group delay needs to be introduced. Group delay is the term given to the ratio of an incremental change in phase shift divided by the associated incremental change in frequency (from calculus, this is the first-derivative). The units for group delay are seconds. If the phase shift is linear, i.e., a constant rate of change per frequency step, then the incremental ratio (first-derivative) will be constant. We therefore refer to a circuit with linear phase shift as having constant group delay.
Group delay is a useful figure of merit for identifying linear phase circuits. Figure 11 shows the group delay response for the Figure 8 low frequency output. Constant group delay extends out to the crossover region where it gradually rolls off (both outputs are identical and sum flat). The summed response is, again, that of a piece of wire.
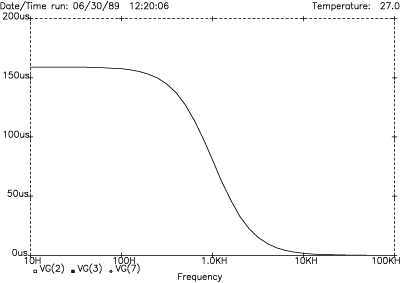
Figure 11. 1st-order low frequency group delay response
The importance of constant group delay is the ability to predict the behavior of the LF output step response. A circuit with constant group delay (linear phase shift) shows no overshoot or associated damping time to a sudden change (step) in input level (Figure 12). The circuit reacts smoothly to the sudden change by rising steadily to meet the new level. It does not go beyond the new level and require time to settle back. We also refer to the step response as the transient response of the circuit. The transient response of the summed outputs is perfect since their sum is perfectly equal to one.
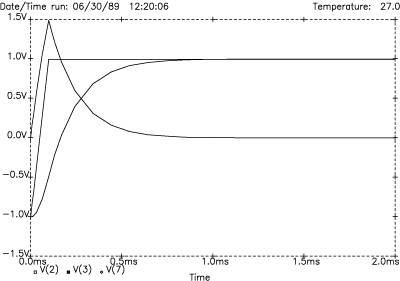
Figure 12. 1st-order transient response
For clarity purposes normally only the step response of the LF network is shown. Nothing is learned by examining the step response of the HF network. A step response represents a transition from one DC level to another DC level, in this case, from -1 volt to +1 volt. A HF network, by definition, does not pass DC (neither does a loudspeaker), so nothing particularly relevant is learned by examining its step response. To illustrate this, Figure 12 shows the HF step response. It begins and ends with zero output since it cannot pass DC. The sharp edge of the input step, however, contains much high frequency material, which the HF network passes. So, it begins at zero, passes the high frequencies as a pulse, and returns to zero.
The HF and LF outputs are the exact complement of each other. Their sum equals the input step exactly as seen in Figure 12. Still, we learn everything we need to know by examining only the LF step response; looking for overshoot and ringing. From now on, just the LF output is shown.
Vector Diagrams
A vector is a graphical thing (now we're getting technical) with magnitude and direction. We can use vectors to produce diagrams representing the instantaneous phase shift and amplitude behavior of electrical circuits. In essence, we freeze the circuit for a moment of time to examine complex relationships.
We shall now apply our two rules to produce a vector diagram showing the relative phase shift and amplitude performance for the 1st-order crossover network at the single crossover frequency (Figure 13a). By convention, 0° points right, +90° points up, -90° points down, and ±180° points left. From Figures 9 & 10 we know the HF output amplitude is -3 dB with +45° of phase shift at 1 kHz, and the LF output is -3 dB with -45° phase shift. Figure 13a represents the vectors as being .707 long (relative to a normalized unity vector) and rotated up and down 45°. This shows us the relative phase difference between the two outputs equals 90°.

Figure 13. 1st-order vector and 2nd-, 3rd- and 4th-order Butterworth vector diagrams
Next we do vector addition to show the summed results. Vector addition involves nothing more complex than mentally moving one of the vectors to the end of the other and connecting the center to this new end point (constructing a parallelogram). Doing this, results in a new vector with a length equal to 1 and an angle of 0°. This tells us the recombined outputs of the HF and LF networks produce constant voltage (i.e., a vector equal to 1), and is in phase with the original input of the circuit (i.e., a vector with 0° phase rotation).
The 1st-order case is ideal when summed. It yields a piece of wire. Since the responses are the exact mirror images of each other, they cancel when summed, thus behaving as if neither was there in the first place. Unfortunately, all optimized higher order versions yield flat voltage/power response, group delay or phase shift, but not all at once. Hence, the existence of different alignments and resultant compromises.
Comparing Butterworth & Linkwitz-Riley Alignments
Butterworth Alignment
There are many types of crossover alignments or filters (most named after mathematicians). Each displays a unique amplitude characteristic throughout the passband. Of these, only Butterworth filters have an absolutely flat amplitude response. For this reason, Butterworth filters are popular for crossover use. Butterworth filters obey our two rules, so we can diagram them for the 2nd, 3rd and 4th-order cases (Figures 13b-13d). The 2nd-order case has ±90° phase shift as shown. This results in the outputs being 180° out of phase. Vector addition for this case produces a zero length vector, or complete cancellation. The popular way around this is to reverse the wiring on one of the drivers (or, if available, electronically inverting the phase at the crossover). This produces a resultant vector 90° out of phase with the input and 3 dB (1.414 equals +3 dB) longer. This means there will be a 3 dB amplitude bump at the crossover region for the combined signals.
The 3rd-order Butterworth case (Figure 13c) mimics the 1st-order case at the crossover frequency, except rotated 180°. Hence, we see the HF vector rotated up 135° (3 x 45°) and the LF vector rotated down the same amount. The phase shift between outputs is still 90°. The resultant is constant voltage (unity) but 180° out-of-phase with the input.
The 4th-order Butterworth diagram (Figure 13d) shows the HF vector rotated up 180° and the LF vector rotated down the same amount. The phase difference between outputs is now zero, but the resultant is +3 dB and 180° out-of-phase with the input. So, the 4th-order and the inverted phase 2nd-order produce 3 dB bumps at the crossover frequency.
Linkwitz-Riley Alignment
Two things characterize a Linkwitz-Riley alignment:
1. In-phase outputs (0° between outputs) at all frequencies (not just at the crossover frequency as popularly believed by some).
2. Constant voltage (the outputs sum to unity at all frequencies).
As discussed earlier Linkwitz-Riley in-phase outputs solve one troublesome aspect of crossover design. The acoustic lobe resulting from both loudspeakers reproducing the same frequency (the crossover frequency) is always on-axis (not tilted up or down) and has no peaking. This is called zero lobing error. In order for this to be true, however, both drivers must be in correct time alignment, i.e., their acoustic centers must lie in the same plane (or electrically put into equivalent alignment by adding time delay to one loudspeaker). Failure to time align the loudspeakers defeats this zero lobing error aspect. (The lobe tilts toward the lagging loudspeaker.)
Examination of Figure 13 shows that the 2nd-order (inverted) and 4th-order Butterworth examples satisfy condition 1, but fail condition 2 since they exhibit a 3 dB peak. So, if a way can be found to make the amplitudes at the crossover point -6 dB instead of -3 dB, then the vector lengths would equal 0.5 (-6 dB) instead of .707 (-3 dB) and sum to unity -- and we would have a Linkwitz-Riley crossover.
Russ Riley suggested cascading (putting in series) two Butterworth filters to create the desired -6 dB crossover points (since each contributes -3 dB). Voila! Linkwitz-Riley alignments were born.
Taken to its most general extremes, cascading any order Butterworth filter produces 2x that order Linkwitz-Riley. Hence, cascading two 1st-order circuits produces a 2nd-order Linkwitz-Riley (LR-2); cascading two 2nd-order Butterworth filters creates a LR-4 design; cascading two 3rd-order Butterworth filters gives a LR-6, and so on. (Starting with LR-2, every other solution requires inverting one output. That is, LR-2 and LR-6 need inverting, while LR-4 and LR-8 do not.)
LR-2, Transient Perfect 2nd-Order Crossover
As an example of this process, let's examine a LR-2 design. Referring to Figure 8 all that is required is to add a buffer amplifier (to avoid interaction between cascaded filter components) to each of these two outputs and then add another resistor/capacitor network identical to the first. We now have a 2nd-order Linkwitz-Riley crossover.
The new vector diagram looks like Figure 14a. Each vector is .5 long (from the fact that each 1st-order reduces by 0.707, and .707 x .707 = .5) with phase angles of ±90°. Since the phase difference equals 180°, we invert one before adding and wind up with a unity vector 90° out of phase with the original.

Figure 14. Linkwitz-Riley vector diagrams for 2nd- to 8th-order cases
Figure 15 shows the amplitude response. The crossover point is located at -6 dB and the slopes are 12 dB/octave (40 dB/decade). The summed response is perfectly flat. Figure 16 shows the phase response. At the crossover frequency we see the HF output (upper trace) has +90° phase shift, while the LF output (lower trace) has -90° phase shift, for a total phase difference of 180°. Invert one before summing and the result is identical to the LF output.
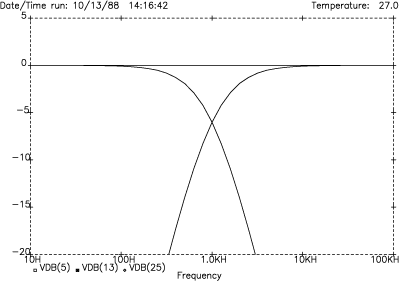
Figure 15. LR-2 amplitude response
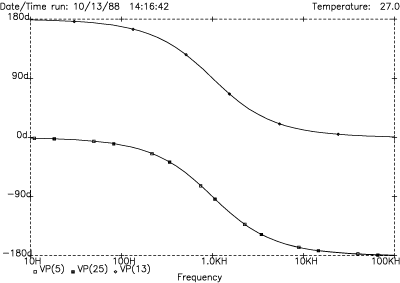
Figure 16. LR-2 phase response
These results differ from the 1st-order case in that the summed results do not yield unity (a piece of wire), but instead create an all-pass network. (An all-pass network is characterized by having a flat amplitude response combined with a smoothly changing phase response.) This illustrates Garde's [10] famous work.
Cascading two linear phase circuits results in linear phase, as shown by the constant group delay plots (all three identical) of Figure 17. And constant group delay gives the transient perfect LF step response shown in Figure 18.
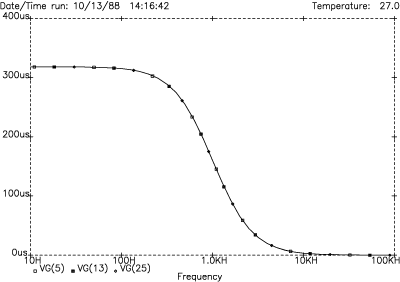
Figure 17. LR-2 group delay
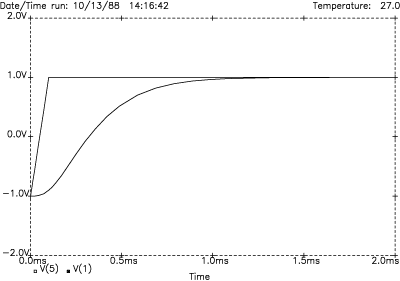
Figure 18. LR-2 transient response
LR-4 and LR-8 Alignments
Looking back to Figure 14b. we see the vector diagrams for 4th and 8th-order Linkwitz-Riley designs. The LR-4 design shows the resultant vector is unity but 180° out of phase with the input at the crossover frequency.
Cascading two 4th-order Butterworth filters results in an 8th-order Linkwitz-Riley design. Figure 14c. shows the vector diagram for the LR-8 case. Here, we see the phase shift for each output undergoes 360° rotation returning to where it began. The resultant vector is back in phase with the original input signal. So, not only are the outputs in phase with each other (for all frequencies), they are also in phase with the input (at the crossover frequency).
8th-Order Comparison
A LR-8 design exhibits slopes of 48 dB/octave, or 160 dB/decade. Figure 19 shows this performance characteristic compared with the LR-4, 4th-order case for reference. As expected, the LR-4 is 80 dB down one decade away from the corner frequency, while the LR-8 is twice that, or 160 dB down. Of interest here, are the potential benefits of narrowing the crossover region by using a LR-8 alignment.
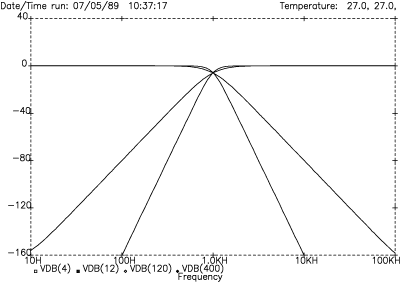
Figure 19. LR-4 and LR-8 slopes
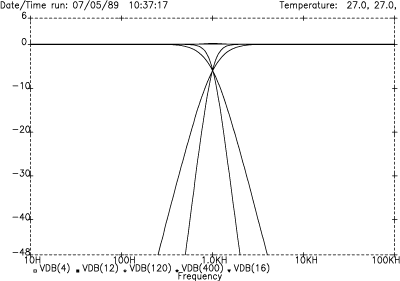
Figure 20. LR-4 and LR-8 slopes magnified
Figure 20 magnifies the responses shown in Figure 19 to reveal a clearer picture of the narrower crossover region, as well as showing the flat summed responses. (The slight difference in summed amplitudes at the crossover frequency is due to a slight gain difference between the two circuits.) The critical crossover region for the LR-8 case is one-half of what it is for the LR-4 case. The exact definition of where the crossover region begins and ends is ambiguous, but, by whatever definition, the region has been halved.
As an example of this, a very conservative definition might be where the responses are 1 dB down from their respective passbands. We would then refer to the crossover region as extending from the -1 dB point on the low-pass response to the -1 dB point on the high-pass response. For LR-8, these points are 769 Hz and 1301 Hz respectively, yielding a crossover region only ¾-octave wide. As a comparative reference, the LR-4 case yields -1 dB points at 591 Hz and 1691 Hz, for a 1.5-octave wide region.
For the LR-8 case, it is interesting to note that the -1 dB point on the low-pass curve corresponds almost exactly to the -20 dB point on the high-pass curve (the exact points occur at 760 Hz and 1316 Hz). So if you want to define the region as where the response is down 20 dB, you get the same answer. The entire region for the LR-8 case is 3/4-octave wide, or it is one-half this number for each driver. That is, the loudspeaker driver (referred to as "driver" from now on) has to be well behaved for only about 0.4-octave beyond the crossover point. This compares with the 4th-order case where the same driver must behave for 0.8-octave.
The above is quite conservative. If other reference points are used, say, the -3 dB points (895 Hz & 1117 Hz), then the LR-8 crossover region is just 1/3-octave wide, and drivers only have to stay linear for 1/6-octave. (1/6-octave away from the crossover frequency the drive signal is attenuated by 12 dB, so the output driver is operating at about 1/16 power.)
The extremely steep slopes offer greater driver protection and linear operation. Beyond the driver's linear limits all frequencies attenuate so quickly that most nonlinearities and interaction ceases being significant. Because of this, the driver need not be as well behaved outside the crossover frequency. It is not required to reproduce frequencies it was not designed for. For similar reasons, power handling capability can be improved for HF drivers as well. And this narrower crossover region lessens the need for precise driver time alignment since the affected spectrum is so small.
The caveat, though, is an increased difficulty in designing good systems with sharp slopes. The loudspeakers involved have differing transient responses, polar patterns and power responses. This means the system designer must know the driver characteristics thoroughly. Ironically, sometimes loudspeaker overlap helps the system blend better even when on-axis amplitude response is flat.
LR-8 Phase Response
Figure 21 shows the respective phase response for LR-4 (upper trace) and LR-8 (lower trace) designs. As predicted by the vector diagram in Figure 14b, the LR-4 case has 180° (4 x 45°) of phase shift at the crossover frequency. Thus, the output signal is out-of-phase with the input signal at the crossover frequency for the LR-4 case. Both outputs are in-phase with each other, but out-of-phase with the input.
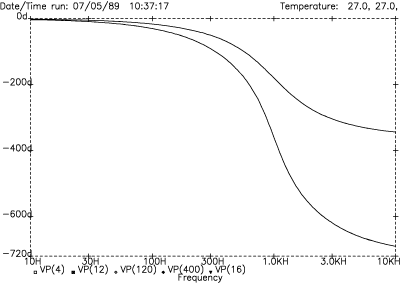
Figure 21. LR-4 and LR-8 phase response
The LR-8 design eliminates this out-of-phase condition by bringing the outputs back in sync with the input signal at the crossover frequency. The lower trace shows the 360° phase shift for the LR-8 alignment.
LR-8 Transient Response
Butterworth functions do not have linear phase shift and consequently do not exhibit constant group delay. (First-order networks are not classified as Butterworth.) Since Linkwitz-Riley designs (higher than LR-2) are cascaded Butterworth, they also do not have constant group delay.
Group delay is just a measure of the non-linearity of phase shift. A direct function of non-linear phase behavior is overshoot and damping time for a step response. The transient behavior of all Linkwitz-Riley designs (greater than 2nd-order) is classic Butterworth in nature. That is, the filters exhibit slight overshoot when responding to a step response, and take time to damp down.
Figure 22 compares LR-8 and LR-4 designs and shows the greater overshoot and damping time for the 8th-order case. The overshoot is 15% for the LR-4 case and twice that, or about 30%, for the LR-8 case. As expected, the LR-8 design takes about twice as long to damp down. The initial rise-time differences are due to the group delay value differences.
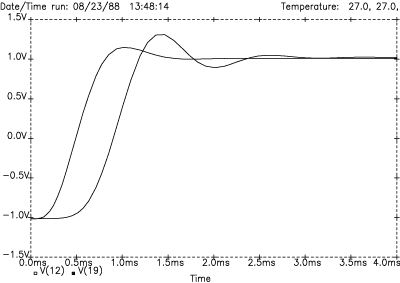
Figure 22. LR-4 and LR-8 transient response
Is It Audible?
The conservative answer says it is not audible to the overwhelming majority of audio professionals. Under laboratory conditions, some people hear a difference on non-musical tones (clicks and square waves).
The practical answer says it is not audible to anyone for real sound systems reproducing real audio signals.
Linkwitz-Riley Power Response
Linkwitz-Riley alignments produce constant voltage response (voltage vectors sum to unity) at the crossover frequency, but they may not produce constant power. At the crossover frequency, each voltage output is half of normal. This produces half the normal current into the loudspeakers. Since power is the product of voltage times current, the power is one-quarter of normal. Considering a simple two-way system, the combined total power at the crossover frequency will be half of normal (one-quarter from each driver), producing a dip of 3 dB at the crossover frequency in the overall power response, provided there is no additional phase shift contributed by the drivers themselves -- such is never the case.
The power response of loudspeakers with noncoincident drivers is a complex problem. See the Vanderkooy and Lipshitz [11] study for complete details.
References
- S. H. Linkwitz "Active Crossover Networks for Non-coincident Drivers," J. Audio Eng. Soc., vol. 24, pp. 2-8 (Jan/Feb 1976).
- D. Bohn. "A Fourth Order State Variable Filter for Linkwitz-Riley Active Crossover Designs," presented at the 74th Convention of the Audio Engineering Society, New York, Oct. 9-12, 1983, preprint no. 2011.
- S. P. Lipshitz and J. Vanderkooy, "A Family of Linear-Phase Crossover Networks of High Slope Derived by Time Delay," J. Audio Eng. Soc., vol. 31, pp. 2-20 (Jan/Feb 1983).
- R. H. Small, "Constant-Voltage Crossover Network Design," J. Audio Eng. Soc., vol. 19, pp. 12-19 (Jan 1971).
- J.R. Ashley and A. L. Kaminsky. "Active and Passive Filters as Loudspeaker Crossover Networks," J. Audio Eng. Soc., vol. 19. pp. 494-502 (June 1971).
- B. B. Bauer, "Audibility of Phase Shift," Wireless World, (Apr. 1974).
- S. P. Lipshitz, M. Pocock, and J. Vanderkooy. "On the Audibility of Midrange Phase Distortion in Audio Systems," J. Audio Eng. Soc., vol. 30, pp. 580-595 (Sep 1982).
- R. Lee. "Is Linear Phase Worthwhile," presented at the 68th Convention of the Audio Engineering Society, Hamburg, Mar 17-20, 1981, preprint no. 1732.
- H. Suzuke, S. Morita and T. Shindo, "On the Perception of Phase Distortion," J. Audio Eng. Soc., vol. 28, no. 9, pp. 570-574 (Sep 1980).
- P. Garde, "All-Pass Crossover Systems," J. Audio Eng. Soc., vol. 28, pp. 575-584 (Sep. 1980).
- J. Vanderkooy & S.P. Lipshitz, "Power Response of Loudspeakers with Noncoincident Drivers -- The Influence of Crossover Design," J. Audio Eng. Soc., Vol. 34, No. 4, pp. 236-244 (Apr. 1986).
![]() "Linkwitz-Riley Crossovers: A Primer" Download this note in PDF.
"Linkwitz-Riley Crossovers: A Primer" Download this note in PDF.