Knowledge Base
Second-Order Digital Filters Done Right
Second-Order Digital Filters Done Right
Ray Miller, DSP Consultant
RaneNote 157, written October 2005
- Numerical Representation
- The Need for Resolution
- Pros and Cons of Floating and Fixed
- Anatomy of a Second-Order Filter
- Noise, Chaos, Limit Cycles
- The Jump Phenomenon
- Fixed-Point Overload
- Frequency Response Errors
- Filter Topologies
Background
Digital filters are capable of excellent performance when done right. If not, they fall prey to a number of problems that will be explored here. They generate noise which is normally extremely small, but may be measurable in certain circumstances. Filters' frequency response curves won't normally match the expected curves exactly, but the difference is usually negligible. Serious potential problems, such as oscillations, are presumably absent in professional audio equipment.
A digital filter is a computer program, typically running in a Digital Signal Processor (DSP) at high enough speed to process audio one sample at a time. Each audio sample is a number and the filter only multiplies, adds, and saves the audio sample and other numbers. The frequency response is controlled by other numbers called coefficients, in place of the resistors and capacitors found in analog filters.
Problems stem from the fact that the numbers must fit into a specific number of bits (binary digits), which places a restriction on the numbers that can be precisely represented, a process called quantization. Multiplication and addition can increase the required number of bits, and errors result from fitting these back to the available number of bits. Results can exceed the representable range, causing overload, or they can require more bits of precision than are available, causing small (quantization) errors. For one example, this occurs when setting the coefficient values, and this results in error in the frequency response.
Numerical Representation
The way numbers are represented is key to understanding the potential problems and their solutions. There are different ways, but all use a binary code, which is a set of bits, each of which is one or zero. Each bit represents a different value, which can be 1, 2, 4, 8, etc, to represent whole numbers, just like decimal uses 1, 10, 100, 1000, etc. For an excellent introduction to binary numbers and audio quantization, see [1]. Alternatively, the values 1/2, 1/4, etc. are used to represent fractional numbers. When this is applied in a straightforward manner it is called fixed-point, referring to the fact that the decimal point doesn't move, that is, each bit always represents the same value. For an example, let's say that there are only two bits. One bit represents 1/2 and the other 1/4. The number represented is the sum of the values indicated by the '1' bits, as shown below:
1/2 |
1/4 |
Value: |
|
0 |
0 |
0 |
|
0 |
1 |
1/4 |
|
1 |
0 |
1/2 |
|
1 |
1 |
3/4 = 1/2 + 1/4 |
The values range from 0 to 3/4. If you use one more bit you can represent twice as many different values, with a resolution of 1/8, ranging from 0 through 7/8. The "first" bit represents the largest value (1/2 here), and is called the Most Significant Bit (MSB). At the other end (1/4 here) is the Least Significant Bit (LSB). If you have a lot of bits you can represent many more values, although in this case they still only range from zero to very close to one. Include negative numbers, and the range of numbers is from negative one to positive one. Although this is a small numeric range, the very fine resolution gives it a large ratiometric range between the largest number that can be represented and the smallest increment (one LSB). For example, 24 bits represents a ratiometric range of 2 to the 24th power, over sixteen million to one, or about 144 dB. Each bit adds approximately 6 dB. Amazingly, this isn't always enough!
When digital filters add and multiply numbers and then force the result back into a fixed number of bits, small errors are generated. Multiplying two numbers can double the number of digits, whether the numbers are whole or not. For instance, 1.23 times 7.89 is 9.7047, and if you can only keep three digits, you will be left with 9.70, resulting in an error of 0.0047. Adding can also increase the number of digits, but only one digit at a time. For example, 9.9 + 9.9 = 19.8. Binary numbers in a DSP have the same characteristics, with bits instead of digits. When each number is within ±1.0, the result of multiplying them is still less than 1.0, and the bits that are discarded are the lowest bits. When adding, there's normally no error, while the programmer has to be aware of when sums can reach 1.0 to prevent exceeding the available range, which is called overflow.
Some DSP families support floating-point, a scheme that uses some bits to choose one of many numeric scales, and uses the remaining bits to provide resolution in a given scale. Floating-point can represent huge or tiny numbers; it supports an enormous numeric range. Figure 1 shows a simple example of floating-point representation. A number occupies one block from one row of blocks. Each row is a scale and each scale has the same number of possibilities (its resolution). For example, two can be represented by any one of the three yellow blocks containing "2".

Figure 1. An example of floating point representation where one of several scales is used at any given time to represent a number. There are eight possible values in any scale, and chosen scale is identified separately. In this example, two bits can identify one of four scales, and three additional bits choose a value from that scale. The shaded boxes show that some numbers can be represented on multiple scales, while others cannot.
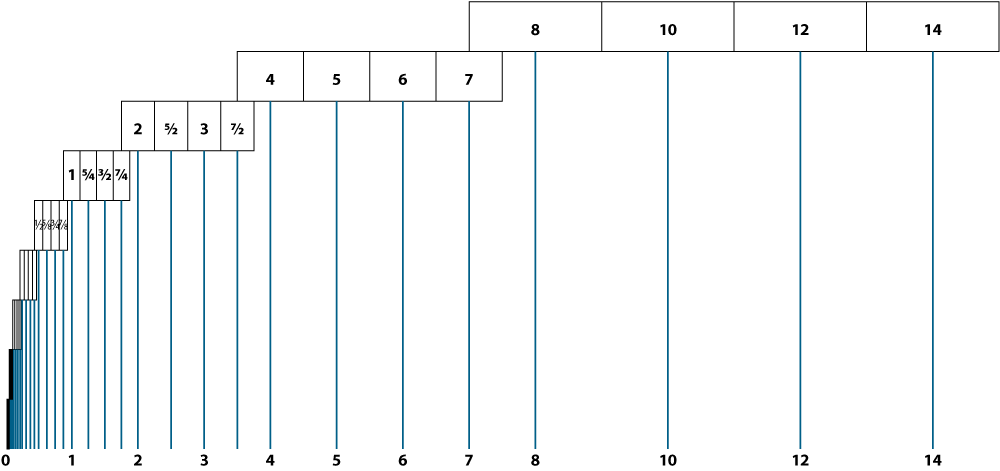
Figure 2. Actual floating point only uses half of each range, with no ambiguity of representation, viewed on a number line.
Figure 2 shows how actual floating point implementations use only the upper half of each scale. There is only one possible representation for a given number. Some bits are used to select a scale, and others to choose a value in that scale. Since only half of each scale is used, one less bit is required to choose the value. A possible shorthand for these bit counts is "total bits"/"value bits." In Figure 2, three bits would be enough to choose the scale, and two for the value: 5/2. A popular floating-point format is 32/24: it occupies 32 bits, using 24 bits for resolution and positive/negative sign (effectively 25), and the rest for the scale. Other popular sizes are 40/33 and 64/53.
The Need for Resolution
Floating-point's range far exceeds the dynamic range of audio signals, and it would be natural to think that this solves all problems. In fact it doesn't because its resolution is limited. This is critical in some instances, particularly with digital filters, when small but significant numbers combine with large numbers. Because large numbers force the floating-point scale up, the difference between representable values is correspondingly increased. Errors are then larger, and if a small number must be added to the large number, it will lose precision or even vanish completely (see [2] for further explanation). The answer is more resolution, in either fixed or floating-point.
How much resolution is needed? For mixing, 24 bits is plenty, however for low-noise audio filters, 24 bits have been shown to be inadequate [3,4]. The reasons are explored below. One remedy is to use a double-precision mode, allowing a DSP with 24 bits to process at 48 bits, or by using a DSP with a higher resolution, such as 32-bit. Forty-bit floating-point with 33 bits of resolution appears to perform very well.
Some Pros and Cons of Floating and Fixed
There are many good arguments for both floating-point and fixed-point. Some of them relate to dynamic range and cost.
Overload (from numerical overflow) is prevented by floating-point's huge dynamic range. This is a significant advantage for digital filters, since techniques for dealing with fixed-point overload require additional code.
Curiously, dynamic range can also be a disadvantage. If gain structure is not set up carefully, signals entering a floating-point mixer may be at drastically different levels, and thereby lost or distorted [2]. To be fair, this is also possible to a lesser extent with fixed-point, and can be avoided with a little care.
Floating-point uses bits for selecting a scale that could have been used instead to increase resolution, and it comes with higher cost and power consumption. As technology advances these differences will become less relevant. Currently the implementation of processing blocks is more cost-effective using fixed-point, but if a very large number of filters is required the comparison begins to tilt in favor of floating-point, where filters are implemented more efficiently. A fair comparison includes the mix of processing block types.
Other pros and cons are related to specific misbehaviors, and will be covered as these problems are discussed.
Anatomy of a Second-Order Filter
A digital filter operates on discrete audio samples and generates output samples. There are many ways to make a filter (filter topologies), and each one trades off various advantages and disadvantages. The simplest second-order digital filter, called a direct form, applies only five multiplies and five additions per sample, applied to five numbers: the input sample, the last two input samples, and the last two output samples. Figure 3 shows an example of this. Second-order corresponds directly to the number of saved input or output samples, with two of each. Every time an input sample is ready, it's saved for future use and is also multiplied by 1.0605. The previous two input samples are multiplied by -1.8144 and 0.8180 respectively. These three products are added together, along with similar products using the previous two outputs. After summing these five products, the result is saved for future calculations and the output sample is ready.
There is a quantization (Q) back to the available number of bits, which takes place before the output history in this example. Placing it here causes several of the filter problems. The optional placement after output history corrects them, with the history holding more bits.
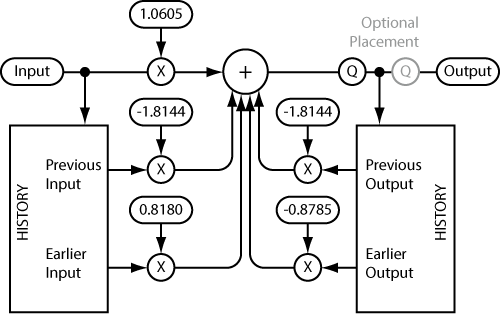
Figure 3. A direct form digital bell filter for 2 kHz, Q = 2, +6 dB, 48 kHz sample rate.
Noise, Chaos, Limit Cycles & the Jump Phenomenon
In many cases the resolution provided by 24 bits can be more than enough, with quantization error around 144 dB down. While this is actually an inharmonic distortion it becomes ordinary noise if there is enough noise already present. It is also chaotic enough to resemble noise if the signal is sufficiently large and complex. Dithering is the application of just the right amount and type of noise before quantization to turn the distortion into noise [5]. It is best to dither, but at the time of this writing dithering isn't always required because few audio signals have even a 120 dB dynamic range, so there is more than enough noise to dither 24 bit (144 dB) samples.
For filters the situation is different because results of earlier calculations are fed back into later calculations; the filter uses previous output values to generate new output values. Errors are actually signals themselves, and it's possible for these signals to grow as they circulate back through. This normally causes noise that can actually become significant.
Filters produce/amplify their quantization noise most at frequencies close to the setting (design) frequency. This effect is greatest when filters are set to low center or cutoff frequencies and high Q [3]. The noise (if audible) will be a low-frequency rumbling.
Another phenomenon is called a limit cycle, which in general is an oscillation, with a frequency that's often not too far from the filter frequency setting. However, in many cases it actually takes the form of a small constant "DC" level. Limit cycles will sustain themselves best without any input signal, and an input signal or noise floor will serve to make them chaotic. They are very undesirable and we should be surprised to find audible limit cycles in professional audio equipment.
Different initial conditions (recent signal history) yield different limit cycles. At lower frequency settings, experiments show that the limit cycle frequency drops and its level increases, and there is then a greater tendency for it to be constant-level rather than oscillation. Higher Q settings are required to bring about oscillation.
Figure 4 shows two examples of limit cycles on the same filter, with slightly different initial conditions. This is the feedback portion of a 400 Hz filter (48 kHz sample rate) with Q = 40.
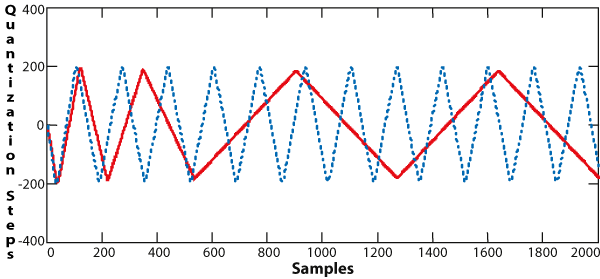
Figure 4. Examples of Limit Cycles
|
On a simple 24-bit fixed-point filter it is possible to start barely audible limit cycles, although it's possible that no product on the market suffers from this. Experiments suggest the following possible procedure for testing filters for limit cycles. Set a bell filter to 200 to 400 Hz, with a Q of 100 if possible. The level setting shouldn't matter much. Alternately apply and mute an input signal of -30 to -60 dBFS with a nearby frequency, using a digital mute so that the filter has zero input. Amplify the output to the point where the noise floor can be heard, preferably using a fast limiter for hearing protection! This can require several attempts, and the limit cycle frequency can be different each time. |
Noise and limit cycles are possible with floating-point, but with different characteristics. While with fixed-point the noise level is fairly constant, with floating-point it is approximately proportional to the signal level. Noise depends on the floating-point scale, and this can shift around, depending on the current audio level and its recent history. Because of noise and distortion from audio converters, filter noise may be difficult or impossible to measure, even with extreme filter settings and a large signal level.
Regardless of resolution, floating-point can normally be expected to have the lowest noise with small signals. But at high signal levels, the scale is brought up and this compromises the floating-point advantage. Based solely on resolution, 32-bit floating-point with 25 effective bits would be 6 dB quieter than 24-bit fixed-point, while actually it has been shown to be quieter still. Bounds from an early comparison are found in [6], but in practice the difference appears to be smaller. Simulations show a floating-point advantage of only about 12 dB with extreme settings. With large signals, double-precision with 24 bits will often be superior to even 40-bit floating-point (40/33), because of the 48 - 33 = 7 more bits of resolution. In any case, with typical filter settings, experiments have shown that noise isn't very significant with 33 or more bits of resolution.
The most likely kind of floating-point limit cycle can be of any size, so it must be prevented completely. One way to prevent it is by using an adequate number of bits [7]. The exact number depends on the particular filter, and is most critical with low-frequency high-Q settings. As an example, even 32-bit floating-point should be free of limit cycles with settings as extreme as 20 Hz, Q=100, depending on implementation. There is another kind of floating-point limit cycle called an underflow limit cycle, but this is extremely small with reasonable filter settings.
Measurement of noise can be difficult. Cascading several filters will bring up the noise level some, most likely by 3 dB for every doubling of filter count. If a large number of filters is cascaded, the result can be deceiving because of a non-flat frequency response. This can be true even if the filters are set to cancel each other, due to errors in the responses themselves.
There are several very effective ways of dealing with noise and limit cycles. Filters can be structured to prevent recirculated errors from being amplified, although this requires more calculation within the filter. Another method is called error feedback, where quantization error itself is used as a signal in the filter, and is employed to compensate the error amplification.
A very simple and effective technique is to make recirculating errors arbitrarily small by increasing the number of bits used in the feedback loop. This is equivalent to optimal error feedback [3,8]. Double-precision can be applied judiciously to minimize the extra calculation involved, which can be three to five times as much. Since double-precision is needed most in the feedback loop, the rest of the filter can be left alone. When this is done with a 24-bit DSP, the errors are reduced by about 138 dB (23 additional bits are typically achieved), placing them well below the noise floor. This is what Rane does to keep second-order filters quiet.
Quantization error can also cause the jump phenomenon [8], where at low signal levels the filter stops filtering properly: the output level becomes unstable, jumping to different gain levels and exhibiting chaotic behavior as the input level changes. This is also considered to be a "forced" limit cycle. Increasing the signal level will cause the filter to return to normal. This problem disappears with enough bits of resolution, such as with 24-bit double-precision. Figure 5 shows an example where the input signal is supposed to be boosted 6 dB, which it is until its level drops. This filter is a 480 Hz, +6 dB bell filter (48 kHz sample rate), Q = 2.1, with 24-bit signed arithmetic. Notice that initially the output (red) is twice the amplitude of the input (blue), until it drops to the point where the output is somewhat erratic. When the input is raised slightly the output follows it without gain but with a small offset. These cases are fairly typical. Raising the input level will return the filter to normal operation.
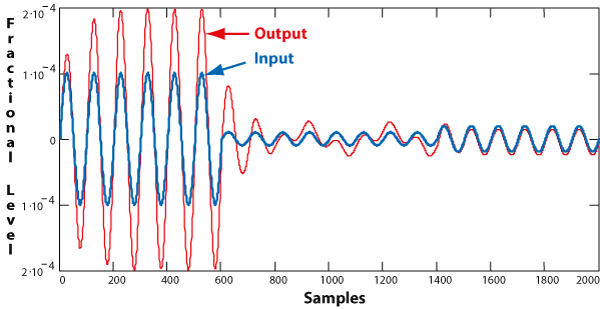
Figure 5. Examples of the Jump Phenomenon
Overload
Fixed-point filters are subject to overload (overflow). Digital overload often sounds much like analog clipping, but this changes dramatically when high frequencies are clipped. Unpleasant inharmonic components rise to audible levels. A filter can be allowed to generate full-scale oscillations during overload, and these can persist even when the audio level driving the filter is reduced.
There are two types of these oscillations: one is a full-scale limit cycle that occurs when excessive output values are not clipped, but instead "wrap around." This refers to a characteristic of a signed number encoding (called twos complement), where increasing a value beyond its range causes it to suddenly change sign. Even if oscillation doesn't happen, the "wrapping around" sounds awful; modern DSP design allows us to prevent this very simply by clipping the output values to their extremes (saturation).
Even with saturation there can be forced overflow oscillation [8], which is a special case of the jump phenomenon, where clipping during overload results in the filter oscillating, often at the input frequency. This happens when a low frequency high Q filter is fed a frequency above its center frequency to the point of overload, and requires 6 dB or more of reduction to recover. Input frequencies below the center frequency also cause oscillations but the filter recovers as soon as the input is reduced. This phenomenon is prevented in different ways, one of which is simply to attenuate the input to the filter so that it doesn't overload.
When testing for overload problems, it's easy to cause clipping before (or after) the filter without overloading the filter itself. If the input signal is near full-scale but not clipped with no filter gain, increasing the filter gain will overload the filter. Be aware that it may then cause overload downstream.
Frequency Response Errors: Coefficient Quantization & Warping
Digital filter frequency response itself is subject to error, which is usually small enough to be inaudible. Often it's not shown in control software graphs. The topology and coefficients determine the frequency response of the filter. Large changes in settings often translate into small changes in coefficients. Conversely, small errors in coefficients can translate into large errors in the response. Errors result from the finite precision, present in both fixed and floating-point. In the example in Figure 3, the value 1.0605 is rounded from 1.06048457 (which is also approximate), and since these determine the frequency response, there will be an error in that response itself. In the example, the result is about 2001.4 Hz, with Q = 2.002 and 6.003 dB. However, if the filter is set to 20 Hz and Q = 10, rounding to the same number of digits yields 41.8 Hz, Q = 20.3, 4.8 dB!
Also, the coefficients are often larger than the fixed-point range of ±1 required by fixed-point, as they are in the example. Then they have to be scaled smaller, usually by 1/2 or 1/4 (losing LSBs) with compensation for this within the filter. Scaling further increases frequency response errors.
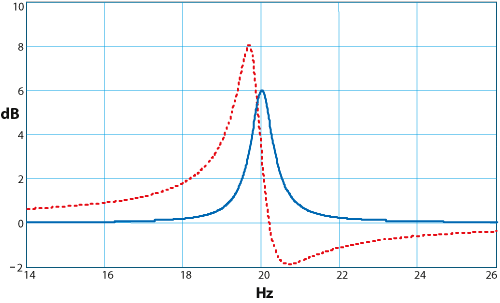
Figure 6. Response Error
Coefficient errors can alter not only the parameters such as center frequency, Q, and peak level, but also the response shape, producing a "tilting" and a second peak. A typical example is shown in Figure 6, with f = 20 Hz, Q = 40, +6 dB, at 48 kHz with values scaled by 1/2 in 24 bits. In extreme cases the response can even be unusable, and this can appear only for certain combinations of settings. For example, instead of a small cut of 3 dB, the result might be a 12 dB boost next to a 12 dB cut! Like the other problems, this is most likely to happen for settings of lowest frequency and highest Q. Manufacturers who allow, for example, a 20 Hz center frequency with a Q of 400 should be sure that these nasty things don't happen, and that isn't always the case! In fairness, such an extreme filter is probably never needed, but in practical cases there can still be some "skew" of the filter shape and/or a moderate design (center or edge) frequency error.
These errors demand serious attention when there are less than 33 bits of resolution, and some extreme settings yield measurable error with 33 bits. Remember that 32-bit floating-point has only 25 bits of resolution, so in general the response error can be severe. Only if all coefficients were close to zero would floating point wield an advantage, but this wouldn't be a useful filter. Other filter topologies are very effective at reducing sensitivity to coefficient errors, especially the Normal form covered below. At Rane we use a proprietary technique to control the filter shape, with only 24 bits.
One problem is related to sample rate rather than quantization. Digital filters operate only within a frequency range of up to half the sample rate. At that frequency and above, there is no frequency response. Just below this the response doesn't usually match the analog response very well, although there are methods for approximating this more closely. Typically there will be some "warping," with the most obvious effect being a narrowing of bandwidth. This can best be dealt with by increasing the sample rate. One alternative that Rane uses is to adjust the bandwidth as the frequency setting is increased [9].
Coefficient Calculation & Ramping
In textbooks, filter coefficients are almost always fixed numbers, while for audio applications filter settings usually need to be manipulated. These changes can be instantaneous or they can be slowly varied from one setting to the next. Naturally, an instantaneous change is much easier (and much less costly) to implement, and in practice this rarely causes a problem. However, if the change is drastic enough and if there is audio present, there is a small chance of a significant transient, and this problem has been studied some [10,11]. Curiously, in [10] the direct form filter is shown to exhibit bizarre behavior when ramped. This behavior didn't appear in equivalent simulations by the author and it has not been a problem in actual products. In any case, it is best to ramp reasonably slowly if the higher cost of ramping is tolerable.
There are several popular ways to ramp, the most straightforward being to ramp the settings and redesign the filter (convert settings to coefficients) every sample. This is costly because it usually takes longer to design the filter than to run it for one sample. Designing the filter less often introduces annoying artifacts, particularly if the design rate is in the most audible range. At low rates the result is zipper noise, and at high rates this results in a tone that may be audible. It might be masked by complex musical passages, and is most likely heard in the presence of a low frequency signal at a high level.
Another way to ramp is to interpolate the coefficients themselves between two designs/settings, which requires much less calculation. The filter near the middle of the interpolation won't be exactly the same as if we were interpolating the settings. In some cases this could cause the filter to become unstable, but this is not the case for the direct form filters, and this technique works very well as long as the interpolating range is small.
When ramping is done quickly, it approaches an instantaneous change, and transients and other behavior begin to appear. The maximum tolerable ramp rate depends on the filter center frequency and bandwidth, as well as the frequency content of the audio signal. A very good compromise can be had where there are no audible transients and the rate is still fairly fast.
At Rane we have sometimes used a hybrid method that combines filter redesign at a low rate and coefficient interpolation at a higher rate, achieving accuracy with high efficiency. This is more work to implement, but proves very effective.
Filter Topologies
The direct form mentioned above is actually a family of four similar types. Two of them are popular, the Direct Form 1 (shown above) and to a lesser extent Direct Form 2 Transpose, because of their efficiency and favorable noise and overload characteristics for fixed-point DSP [3,8]. Other topologies are quieter, but even the quietest can't be used in the most demanding applications without modification [3,12].
The quietest topology is called the Normal, Coupled, or Gold-Rader type, which when properly implemented has minimal noise and very low sensitivity to coefficient quantization. It does require significant computation and its noise is higher than simply using first-order error feedback with direct-form [3]. Use of more bits can, of course, remedy this. Calculating the filter coefficients is also more difficult than for direct-form.
In almost every case, when this filter is described, only the recursive (feedback) portion is covered, and the (nonrecursive) rest of the filter ignored. The nonrecursive portion has been included in [3], but this particular topology adds one sample of delay and greatly increases sensitivity to coefficient quantization. For the original topology see [13] (also briefly covered in [14]), but be prepared for complicated design equations.
Another interesting topology is the Embedded All-Pass, where settings translate more directly into the coefficients [15,16]. This best supports the bell filter type, and doesn't readily support other types, such as low-pass or second-order shelving.
Another topology is the Ladder filter. Although it has many good characteristics, it needs a great deal of input attenuation to prevent overload in normal operation [17], reducing the dynamic range. It also requires a lot of computation, and is best suited for the bell filter type.
There are other topologies, but they require more calculation than the direct form, and like the direct form, they can't generally be used for professional audio without the use of error feedback, 24-bit double precision, or 40-bit floating-point. Some of them may still be useful in certain applications.
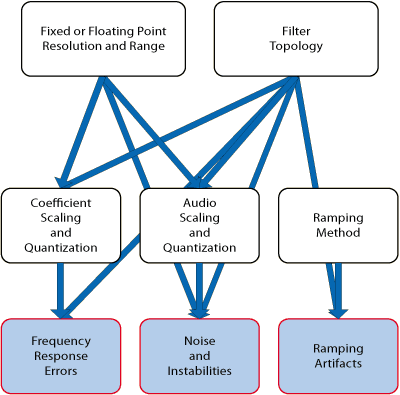
Figure 7. Summary of the Origins of Filter Problems
Conclusions
There are many pitfalls and solutions in digital filtering, some of which are more likely to be measurable. Noise, frequency response errors, and transients due to fast filter design changes are likely to be present to some small degree. Limit cycles, overflow oscillations, and the jump phenomenon are less likely but may occur. Except for high-frequency response warping, revealing any problems requires low frequency settings along with the highest Q, such as a sharp low frequency notch filter. It is difficult or impossible to measure these errors in properly designed equipment, but knowledge of the issues helps in identifying problems when they do occur.
No topology solves all problems. High resolution is key, achieved by additional coding or by using a different processor. Proper design should support all filter settings, and this requires more than 24-bit fixed-point or 32-bit floating-point.
Rane uses fixed-point direct form filters with double precision feedback, resulting in extremely low noise and high reliability. Moderate input attenuation provides protection from overflow oscillations. We do all of this while remaining cost-competitive.
References
- Dennis Bohn, RaneNote "Digital Dharma of Audio A/D Converters" 2004
- Greg Duckett, Terry Pennington, RaneNote "Fixed-Point vs Floating-Point DSP for Superior Audio" 2002
- Rhonda Wilson, "Filter Topologies," JAES Vol. 41, No. 9, Sept 1993.
- Wei Chen, "Performance of Cascade and Parallel IIR Filters," JAES Vol. 44, No. 3, Mar 1996
- John Vanderkooy, Stanley P. Lipshitz, "Dither in Digital Audio," JAES Vol 35, No. 12, Dec. 1987
- Clifford Weinstein, Alan Oppenheim, "A Comparison of Roundoff Noise in Floating Point and Fixed Point Digital Filter Realizations," Proc. IEEE (Letters), vol. 57, June 1969
- Timo Laakso, Bing Zeng, "Limit Cycles in Floating-Pont Implementations of Recursive Filters -- A Review," Proc. IEEE Int. Symp. on Circuits and Systems , pp.1816-1819, San Diego, California, May 10-13 1992.
- Jon Dattorro, "The Implementation of Recursive Digital Filters for High-Fidelity Audio," JAES Vol. 36, No. 11, Nov 1988
- Robert Bristow-Johnson, "The Equivalence of Various Methods of Computing Biquad Coefficients for Audio Parametric Equalizers," AES preprint 3906, Oct. 1994.
- James A Moorer, "48-Bit Integer Processing Beats 32-Bit Floating Point for Professional Audio Applications," AES Preprint 5038, Sept. 1999.
- Rob Clark, Emmanuel Ifeachor, Glenn Rogers, "Filter Morphing -- Topologies, Signals and Sampling Rates," AES Preprint 5661, Oct 2002
- Duane Wise, "A Tutorial on Performance Metrics and Noise Propagation in Digital IIR Filters," AES Preprint 5470, Sept. 2001
- Richard Roberts and Clifford Mullis, "Digital Signal Processing," Addison Wesley Inc, Reading, MA, 1987
- Richard Cabot, "Performance Limitations of Digital Filter Architectures," AES Preprint 2964, Aug. 1990.
- Udo Zolzer, Thomas Boltze, "Parametric Digital Filter Structures," AES Preprint 4099, Oct. 1995.
- Fred Harris, Eric Brooking, "A Versatile Parametric Filter Using an Imbedded All-Pass Sub-Filter to Independently Adjust Bandwidth, Center Frequency, and Boost or Cut," AES Preprint 3757, Oct. 1993.
- Dana Massie, "An Engineering Study of the 4-Multiply Normalized Ladder Filter," AES Preprint 3187, Oct. 1991.
![]() "Second-Order Digital Filters Done Right" Download this note in PDF.
"Second-Order Digital Filters Done Right" Download this note in PDF.